Group Theory via Category Theory
$begingroup$
I have previously done a course on group theory and now I am doing a reading course on category theory. So as an interesting exercise I have been asked to write an exposition of group theory for someone who already knows category theory but doesn't know any group theory. I have been given the liberty to decide how I build the theory. I already have a vague idea of what is to be done.
- However, I would like to hear ideas about what should be done. So I solicit advice on things I should emphasize, the ways I can exploit the given familiarity with category theory for a more economic presentation and/or a exposition through "the path of least resistance". And please feel free to also mention any tips or precautions.
- Please refer me to material along this line.
Thanks!
group-theory category-theory
$endgroup$
add a comment |
$begingroup$
I have previously done a course on group theory and now I am doing a reading course on category theory. So as an interesting exercise I have been asked to write an exposition of group theory for someone who already knows category theory but doesn't know any group theory. I have been given the liberty to decide how I build the theory. I already have a vague idea of what is to be done.
- However, I would like to hear ideas about what should be done. So I solicit advice on things I should emphasize, the ways I can exploit the given familiarity with category theory for a more economic presentation and/or a exposition through "the path of least resistance". And please feel free to also mention any tips or precautions.
- Please refer me to material along this line.
Thanks!
group-theory category-theory
$endgroup$
$begingroup$
Quite an odd hypothetical person - I imagine most people who know category theory studied abstract algebra before it.
$endgroup$
– rlms
Jan 9 '15 at 20:51
6
$begingroup$
@sweeneyrod, many people find themselves needing to revise abstract algebra "essentially from the beginning" though, despite knowing more advanced material.
$endgroup$
– goblin
Jan 10 '15 at 3:47
$begingroup$
@sweeneyrod, Maybe (finally!) category theory is coming first (possibly via computer science)
$endgroup$
– Jérôme JEAN-CHARLES
Aug 10 '15 at 13:48
$begingroup$
I think you'll find An Invitation to General Algebra and Universal Constructions useful. The title should make the reason obvious.
$endgroup$
– M. Vinay
Jan 22 '16 at 3:55
$begingroup$
@sweeneyrod Well, it is not hypothetical. I am an example. I learned about limits and adjunctions before learning, what a centralizer is.
$endgroup$
– Stefan Perko
Jan 23 '17 at 21:47
add a comment |
$begingroup$
I have previously done a course on group theory and now I am doing a reading course on category theory. So as an interesting exercise I have been asked to write an exposition of group theory for someone who already knows category theory but doesn't know any group theory. I have been given the liberty to decide how I build the theory. I already have a vague idea of what is to be done.
- However, I would like to hear ideas about what should be done. So I solicit advice on things I should emphasize, the ways I can exploit the given familiarity with category theory for a more economic presentation and/or a exposition through "the path of least resistance". And please feel free to also mention any tips or precautions.
- Please refer me to material along this line.
Thanks!
group-theory category-theory
$endgroup$
I have previously done a course on group theory and now I am doing a reading course on category theory. So as an interesting exercise I have been asked to write an exposition of group theory for someone who already knows category theory but doesn't know any group theory. I have been given the liberty to decide how I build the theory. I already have a vague idea of what is to be done.
- However, I would like to hear ideas about what should be done. So I solicit advice on things I should emphasize, the ways I can exploit the given familiarity with category theory for a more economic presentation and/or a exposition through "the path of least resistance". And please feel free to also mention any tips or precautions.
- Please refer me to material along this line.
Thanks!
group-theory category-theory
group-theory category-theory
asked Jan 9 '15 at 13:05
Inspired_BlueInspired_Blue
24517
24517
$begingroup$
Quite an odd hypothetical person - I imagine most people who know category theory studied abstract algebra before it.
$endgroup$
– rlms
Jan 9 '15 at 20:51
6
$begingroup$
@sweeneyrod, many people find themselves needing to revise abstract algebra "essentially from the beginning" though, despite knowing more advanced material.
$endgroup$
– goblin
Jan 10 '15 at 3:47
$begingroup$
@sweeneyrod, Maybe (finally!) category theory is coming first (possibly via computer science)
$endgroup$
– Jérôme JEAN-CHARLES
Aug 10 '15 at 13:48
$begingroup$
I think you'll find An Invitation to General Algebra and Universal Constructions useful. The title should make the reason obvious.
$endgroup$
– M. Vinay
Jan 22 '16 at 3:55
$begingroup$
@sweeneyrod Well, it is not hypothetical. I am an example. I learned about limits and adjunctions before learning, what a centralizer is.
$endgroup$
– Stefan Perko
Jan 23 '17 at 21:47
add a comment |
$begingroup$
Quite an odd hypothetical person - I imagine most people who know category theory studied abstract algebra before it.
$endgroup$
– rlms
Jan 9 '15 at 20:51
6
$begingroup$
@sweeneyrod, many people find themselves needing to revise abstract algebra "essentially from the beginning" though, despite knowing more advanced material.
$endgroup$
– goblin
Jan 10 '15 at 3:47
$begingroup$
@sweeneyrod, Maybe (finally!) category theory is coming first (possibly via computer science)
$endgroup$
– Jérôme JEAN-CHARLES
Aug 10 '15 at 13:48
$begingroup$
I think you'll find An Invitation to General Algebra and Universal Constructions useful. The title should make the reason obvious.
$endgroup$
– M. Vinay
Jan 22 '16 at 3:55
$begingroup$
@sweeneyrod Well, it is not hypothetical. I am an example. I learned about limits and adjunctions before learning, what a centralizer is.
$endgroup$
– Stefan Perko
Jan 23 '17 at 21:47
$begingroup$
Quite an odd hypothetical person - I imagine most people who know category theory studied abstract algebra before it.
$endgroup$
– rlms
Jan 9 '15 at 20:51
$begingroup$
Quite an odd hypothetical person - I imagine most people who know category theory studied abstract algebra before it.
$endgroup$
– rlms
Jan 9 '15 at 20:51
6
6
$begingroup$
@sweeneyrod, many people find themselves needing to revise abstract algebra "essentially from the beginning" though, despite knowing more advanced material.
$endgroup$
– goblin
Jan 10 '15 at 3:47
$begingroup$
@sweeneyrod, many people find themselves needing to revise abstract algebra "essentially from the beginning" though, despite knowing more advanced material.
$endgroup$
– goblin
Jan 10 '15 at 3:47
$begingroup$
@sweeneyrod, Maybe (finally!) category theory is coming first (possibly via computer science)
$endgroup$
– Jérôme JEAN-CHARLES
Aug 10 '15 at 13:48
$begingroup$
@sweeneyrod, Maybe (finally!) category theory is coming first (possibly via computer science)
$endgroup$
– Jérôme JEAN-CHARLES
Aug 10 '15 at 13:48
$begingroup$
I think you'll find An Invitation to General Algebra and Universal Constructions useful. The title should make the reason obvious.
$endgroup$
– M. Vinay
Jan 22 '16 at 3:55
$begingroup$
I think you'll find An Invitation to General Algebra and Universal Constructions useful. The title should make the reason obvious.
$endgroup$
– M. Vinay
Jan 22 '16 at 3:55
$begingroup$
@sweeneyrod Well, it is not hypothetical. I am an example. I learned about limits and adjunctions before learning, what a centralizer is.
$endgroup$
– Stefan Perko
Jan 23 '17 at 21:47
$begingroup$
@sweeneyrod Well, it is not hypothetical. I am an example. I learned about limits and adjunctions before learning, what a centralizer is.
$endgroup$
– Stefan Perko
Jan 23 '17 at 21:47
add a comment |
4 Answers
4
active
oldest
votes
$begingroup$
Here's some food for thought (although its nowhere near enough material):
A groupoid is a category in which every morphism is an isomorphism (i.e. all morphisms are invertible). Groupoids are an oidification of the concept "group"; in other words, a group is just a one-object groupoid.
The inclusion $mathbf{Grp} hookrightarrow mathbf{Grpd}$ does not preserve coproducts. Hence the coproduct of groups is part of what gives group-theory its own special flavour, distinct from the flavour of groupoid theory. (Perhaps use the wedge sum of nice topological spaces to motivate the group-theoretic coproduct in its own right, since the fundamental group of a wedge sum is the coproduct of the fundamental groups under certain general conditions.)
A group is just a connected groupoid, up to equivalence. Hence every (small) groupoid is the (groupoid-theoretic) coproduct of a set-indexed family of groups, up to equivalence. Looking at it another way, groups are kind of like the "atoms" from which we can build up any groupoid. (Note that the same relationship does not hold between monoids and categories.)
Let $mathbf{C}$ denote a category. Then the isomorphisms of $mathbf{C}$ form a groupoid called the core of $mathbf{C}$, typically denoted $mathrm{core}(mathbf{C}).$ Now consider the automorphism function $mathrm{Aut}_mathbf{C} : mathrm{Obj}(mathbf{C}) rightarrow mathbf{Grp}$ that takes any object $X$ of $mathbf{C}$ to its group of automorphisms $mathrm{Aut}_mathbf{C}(X).$ This cannot be regarded as a functor out of $mathbf{C}$ in any sensible way. However, it can be regarded as a functor out of $mathrm{core}(mathbf{C})$.
The action of a group $G$ on a set (a "$G$-set") is precisely an object of the functor category
$[G,mathbf{Set}].$ More generally, the action of a group $G$ on a
"foo" is just an object of $[G,mathbf{Foo}]$, where $mathbf{Foo}$
is the category of foos. This makes sense even if $G$ is allowed to
be a general groupoid, or even a general category.
This explains why every homomorphism $varphi : G rightarrow H$ of groups gives rise to a functor $[H,mathbf{Set}] rightarrow [G,mathbf{Set}]$ "going the other way"; its because $mathrm{Hom}$ is contravariant in its first argument.
We may consider group objects in any category with finite products (note that we don't even need finite limits; finite products will do). For example, the group objects in $mathbf{Top}$ (the category of topological spaces) are precisely the topological groups.
Given a monoid $M$, every $M$-set $X$ is associated with a category $tilde{X}$ called its "translation category," defined as follows. The object set of $tilde{X}$ is just the underlying set of $X$. Given objects $x,y in X$, we define that an arrow $x rightarrow y$ is just a pair $(x,m)$ such that $m in M$ and $mx = y$. Composition of arrows is by multiplication. Explicitly:
$$(x,m_y)(y,m_z) = (x,m_z m_y).$$
Furthermore, if $G$ is a group and $X$ is a $G$-set, then the translation category $tilde{X}$ of $X$ is always a groupoid, called the translation groupoid of $X.$ Note also that every monoid acts on itself by left-multiplication. So given a monoid $M$, we may think of $M$ as an $M$-set, and hence we may write $tilde{M}$ and speak of the translation category of $M$. As a special case, if $G$ is a group, we may write $tilde{G}$ and speak of the translation groupoid of $G$.
For something a little more advanced, George Bergman has recently shown how to define the concepts of "inner automorphism" and "inner endomorphism" for objects of an arbitrary category. This could be an interesting viewpoint to take in your own report.
$endgroup$
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
add a comment |
$begingroup$
You may want to look at Paolo Aluffi's book called Algebra Chapter zero. He begins talking about categories first and then introduces groups. He says a group is a groupoid (category in which every morphism is invertible) with only one object.
$endgroup$
add a comment |
$begingroup$
On the [sub]topic of bibliography, there is a reasonable chapter (#4) in Steve Awodey's Category Theory book; the chapter introduces group theory with the help of category theory. Awodey is a philosophy prof at CMU, which probably explains why he put such a chapter in his book; the target audience isn't assumed have first learned group theory as the math undergrads normally do. A version of that chapter (probalby the one that appeared in the first edition of the book) is freely available on a CMU class webpage.
$endgroup$
add a comment |
$begingroup$
There are two books which link category theory and group theory via the use of groupoids. A pioneer in this was Philip Higgins, whose 1971 van Nostrand Notes are now available as free download as Categories and Groupoids (T&G). Following Philip's lead I started investigating groupoids in $1$-dimensional homotopy theory in 1965, and concluded that the groupoid point of view made many things clearer. The book I published in 1968 is now in its third edition and available as Topology and Groupoids. A key tool was the fundamental groupoid $pi_1(X,A)$ on a set $A$ of base points, chosen according to the geometry, which dates from 1967. The above are the only undergraduate texts in English using this concept. here is a mathoverview discussion on many base points, and a presentation on the background in algebraic topology was given at Galway in December, 2014. See also my preprint page.
A feature of both of these books is the use of the following construction. Let $G$ be a groupoid with object set $X$ and let $f:X to Y$ be a function to a set $Y$. Then we obtain a new groupoid which can be written $U_f(G)$ with object set $Y$ and a nice universal property. From this can be deduced the construction of coproducts of groups, and of free groups and free groupoids. This goes a long way to covering point 2 of @goblin's comment. Thus there is a combinatorial groupoid theory which in principle includes combinatorial group theory.
January 23, 2017 I should say that "combinatorial groupoid theory" is my own coinage, but also reflects JHC Whitehead's term "combinatorial homotopy theory".
The areas include those mentioned above and also fibrations and covering morphisms, groups acting on groupoids, (see T&G for all these). Other references are in my groupoids web page.
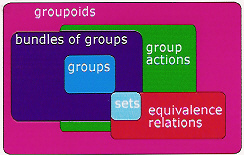
To answer the comment of goblin: how does one obtain a groupoid from a bundle of groups? The latter can be seen as a disjoint family ${G_s: s in S}$ of groups.
The associated groupoid $G$ has object set $S$ and a group $G_s$ for each $S in S$, so that $G(s,t)$ is empty if $s ne t$.
Another feature of the category of groupoids is the variety of morphisms. For groups there are mainly two special kinds of morphisms: injective or surjective. For groupoids we also have fibrations, covering morphisms, universal morphisms, orbit morphisms.
There is a special groupoid $mathcal I$ which has two objects $0,1$ and only one non identity $iota: 0 to 1$, and so also only $iota^{-1}: 1 to 0$. This seems a completely useless kind of object! But it defines a homotopy theory for groupoids, and also plays the same role in the category of groupoids as does the integers $ mathbf Z$ in the category of groups. Further, identifying $0,1$ in $mathcal I$ in the category of groupoids gives the integers $mathbf Z$, which explains the fundamental group of the circle!
$endgroup$
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f1097654%2fgroup-theory-via-category-theory%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
4 Answers
4
active
oldest
votes
4 Answers
4
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Here's some food for thought (although its nowhere near enough material):
A groupoid is a category in which every morphism is an isomorphism (i.e. all morphisms are invertible). Groupoids are an oidification of the concept "group"; in other words, a group is just a one-object groupoid.
The inclusion $mathbf{Grp} hookrightarrow mathbf{Grpd}$ does not preserve coproducts. Hence the coproduct of groups is part of what gives group-theory its own special flavour, distinct from the flavour of groupoid theory. (Perhaps use the wedge sum of nice topological spaces to motivate the group-theoretic coproduct in its own right, since the fundamental group of a wedge sum is the coproduct of the fundamental groups under certain general conditions.)
A group is just a connected groupoid, up to equivalence. Hence every (small) groupoid is the (groupoid-theoretic) coproduct of a set-indexed family of groups, up to equivalence. Looking at it another way, groups are kind of like the "atoms" from which we can build up any groupoid. (Note that the same relationship does not hold between monoids and categories.)
Let $mathbf{C}$ denote a category. Then the isomorphisms of $mathbf{C}$ form a groupoid called the core of $mathbf{C}$, typically denoted $mathrm{core}(mathbf{C}).$ Now consider the automorphism function $mathrm{Aut}_mathbf{C} : mathrm{Obj}(mathbf{C}) rightarrow mathbf{Grp}$ that takes any object $X$ of $mathbf{C}$ to its group of automorphisms $mathrm{Aut}_mathbf{C}(X).$ This cannot be regarded as a functor out of $mathbf{C}$ in any sensible way. However, it can be regarded as a functor out of $mathrm{core}(mathbf{C})$.
The action of a group $G$ on a set (a "$G$-set") is precisely an object of the functor category
$[G,mathbf{Set}].$ More generally, the action of a group $G$ on a
"foo" is just an object of $[G,mathbf{Foo}]$, where $mathbf{Foo}$
is the category of foos. This makes sense even if $G$ is allowed to
be a general groupoid, or even a general category.
This explains why every homomorphism $varphi : G rightarrow H$ of groups gives rise to a functor $[H,mathbf{Set}] rightarrow [G,mathbf{Set}]$ "going the other way"; its because $mathrm{Hom}$ is contravariant in its first argument.
We may consider group objects in any category with finite products (note that we don't even need finite limits; finite products will do). For example, the group objects in $mathbf{Top}$ (the category of topological spaces) are precisely the topological groups.
Given a monoid $M$, every $M$-set $X$ is associated with a category $tilde{X}$ called its "translation category," defined as follows. The object set of $tilde{X}$ is just the underlying set of $X$. Given objects $x,y in X$, we define that an arrow $x rightarrow y$ is just a pair $(x,m)$ such that $m in M$ and $mx = y$. Composition of arrows is by multiplication. Explicitly:
$$(x,m_y)(y,m_z) = (x,m_z m_y).$$
Furthermore, if $G$ is a group and $X$ is a $G$-set, then the translation category $tilde{X}$ of $X$ is always a groupoid, called the translation groupoid of $X.$ Note also that every monoid acts on itself by left-multiplication. So given a monoid $M$, we may think of $M$ as an $M$-set, and hence we may write $tilde{M}$ and speak of the translation category of $M$. As a special case, if $G$ is a group, we may write $tilde{G}$ and speak of the translation groupoid of $G$.
For something a little more advanced, George Bergman has recently shown how to define the concepts of "inner automorphism" and "inner endomorphism" for objects of an arbitrary category. This could be an interesting viewpoint to take in your own report.
$endgroup$
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
add a comment |
$begingroup$
Here's some food for thought (although its nowhere near enough material):
A groupoid is a category in which every morphism is an isomorphism (i.e. all morphisms are invertible). Groupoids are an oidification of the concept "group"; in other words, a group is just a one-object groupoid.
The inclusion $mathbf{Grp} hookrightarrow mathbf{Grpd}$ does not preserve coproducts. Hence the coproduct of groups is part of what gives group-theory its own special flavour, distinct from the flavour of groupoid theory. (Perhaps use the wedge sum of nice topological spaces to motivate the group-theoretic coproduct in its own right, since the fundamental group of a wedge sum is the coproduct of the fundamental groups under certain general conditions.)
A group is just a connected groupoid, up to equivalence. Hence every (small) groupoid is the (groupoid-theoretic) coproduct of a set-indexed family of groups, up to equivalence. Looking at it another way, groups are kind of like the "atoms" from which we can build up any groupoid. (Note that the same relationship does not hold between monoids and categories.)
Let $mathbf{C}$ denote a category. Then the isomorphisms of $mathbf{C}$ form a groupoid called the core of $mathbf{C}$, typically denoted $mathrm{core}(mathbf{C}).$ Now consider the automorphism function $mathrm{Aut}_mathbf{C} : mathrm{Obj}(mathbf{C}) rightarrow mathbf{Grp}$ that takes any object $X$ of $mathbf{C}$ to its group of automorphisms $mathrm{Aut}_mathbf{C}(X).$ This cannot be regarded as a functor out of $mathbf{C}$ in any sensible way. However, it can be regarded as a functor out of $mathrm{core}(mathbf{C})$.
The action of a group $G$ on a set (a "$G$-set") is precisely an object of the functor category
$[G,mathbf{Set}].$ More generally, the action of a group $G$ on a
"foo" is just an object of $[G,mathbf{Foo}]$, where $mathbf{Foo}$
is the category of foos. This makes sense even if $G$ is allowed to
be a general groupoid, or even a general category.
This explains why every homomorphism $varphi : G rightarrow H$ of groups gives rise to a functor $[H,mathbf{Set}] rightarrow [G,mathbf{Set}]$ "going the other way"; its because $mathrm{Hom}$ is contravariant in its first argument.
We may consider group objects in any category with finite products (note that we don't even need finite limits; finite products will do). For example, the group objects in $mathbf{Top}$ (the category of topological spaces) are precisely the topological groups.
Given a monoid $M$, every $M$-set $X$ is associated with a category $tilde{X}$ called its "translation category," defined as follows. The object set of $tilde{X}$ is just the underlying set of $X$. Given objects $x,y in X$, we define that an arrow $x rightarrow y$ is just a pair $(x,m)$ such that $m in M$ and $mx = y$. Composition of arrows is by multiplication. Explicitly:
$$(x,m_y)(y,m_z) = (x,m_z m_y).$$
Furthermore, if $G$ is a group and $X$ is a $G$-set, then the translation category $tilde{X}$ of $X$ is always a groupoid, called the translation groupoid of $X.$ Note also that every monoid acts on itself by left-multiplication. So given a monoid $M$, we may think of $M$ as an $M$-set, and hence we may write $tilde{M}$ and speak of the translation category of $M$. As a special case, if $G$ is a group, we may write $tilde{G}$ and speak of the translation groupoid of $G$.
For something a little more advanced, George Bergman has recently shown how to define the concepts of "inner automorphism" and "inner endomorphism" for objects of an arbitrary category. This could be an interesting viewpoint to take in your own report.
$endgroup$
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
add a comment |
$begingroup$
Here's some food for thought (although its nowhere near enough material):
A groupoid is a category in which every morphism is an isomorphism (i.e. all morphisms are invertible). Groupoids are an oidification of the concept "group"; in other words, a group is just a one-object groupoid.
The inclusion $mathbf{Grp} hookrightarrow mathbf{Grpd}$ does not preserve coproducts. Hence the coproduct of groups is part of what gives group-theory its own special flavour, distinct from the flavour of groupoid theory. (Perhaps use the wedge sum of nice topological spaces to motivate the group-theoretic coproduct in its own right, since the fundamental group of a wedge sum is the coproduct of the fundamental groups under certain general conditions.)
A group is just a connected groupoid, up to equivalence. Hence every (small) groupoid is the (groupoid-theoretic) coproduct of a set-indexed family of groups, up to equivalence. Looking at it another way, groups are kind of like the "atoms" from which we can build up any groupoid. (Note that the same relationship does not hold between monoids and categories.)
Let $mathbf{C}$ denote a category. Then the isomorphisms of $mathbf{C}$ form a groupoid called the core of $mathbf{C}$, typically denoted $mathrm{core}(mathbf{C}).$ Now consider the automorphism function $mathrm{Aut}_mathbf{C} : mathrm{Obj}(mathbf{C}) rightarrow mathbf{Grp}$ that takes any object $X$ of $mathbf{C}$ to its group of automorphisms $mathrm{Aut}_mathbf{C}(X).$ This cannot be regarded as a functor out of $mathbf{C}$ in any sensible way. However, it can be regarded as a functor out of $mathrm{core}(mathbf{C})$.
The action of a group $G$ on a set (a "$G$-set") is precisely an object of the functor category
$[G,mathbf{Set}].$ More generally, the action of a group $G$ on a
"foo" is just an object of $[G,mathbf{Foo}]$, where $mathbf{Foo}$
is the category of foos. This makes sense even if $G$ is allowed to
be a general groupoid, or even a general category.
This explains why every homomorphism $varphi : G rightarrow H$ of groups gives rise to a functor $[H,mathbf{Set}] rightarrow [G,mathbf{Set}]$ "going the other way"; its because $mathrm{Hom}$ is contravariant in its first argument.
We may consider group objects in any category with finite products (note that we don't even need finite limits; finite products will do). For example, the group objects in $mathbf{Top}$ (the category of topological spaces) are precisely the topological groups.
Given a monoid $M$, every $M$-set $X$ is associated with a category $tilde{X}$ called its "translation category," defined as follows. The object set of $tilde{X}$ is just the underlying set of $X$. Given objects $x,y in X$, we define that an arrow $x rightarrow y$ is just a pair $(x,m)$ such that $m in M$ and $mx = y$. Composition of arrows is by multiplication. Explicitly:
$$(x,m_y)(y,m_z) = (x,m_z m_y).$$
Furthermore, if $G$ is a group and $X$ is a $G$-set, then the translation category $tilde{X}$ of $X$ is always a groupoid, called the translation groupoid of $X.$ Note also that every monoid acts on itself by left-multiplication. So given a monoid $M$, we may think of $M$ as an $M$-set, and hence we may write $tilde{M}$ and speak of the translation category of $M$. As a special case, if $G$ is a group, we may write $tilde{G}$ and speak of the translation groupoid of $G$.
For something a little more advanced, George Bergman has recently shown how to define the concepts of "inner automorphism" and "inner endomorphism" for objects of an arbitrary category. This could be an interesting viewpoint to take in your own report.
$endgroup$
Here's some food for thought (although its nowhere near enough material):
A groupoid is a category in which every morphism is an isomorphism (i.e. all morphisms are invertible). Groupoids are an oidification of the concept "group"; in other words, a group is just a one-object groupoid.
The inclusion $mathbf{Grp} hookrightarrow mathbf{Grpd}$ does not preserve coproducts. Hence the coproduct of groups is part of what gives group-theory its own special flavour, distinct from the flavour of groupoid theory. (Perhaps use the wedge sum of nice topological spaces to motivate the group-theoretic coproduct in its own right, since the fundamental group of a wedge sum is the coproduct of the fundamental groups under certain general conditions.)
A group is just a connected groupoid, up to equivalence. Hence every (small) groupoid is the (groupoid-theoretic) coproduct of a set-indexed family of groups, up to equivalence. Looking at it another way, groups are kind of like the "atoms" from which we can build up any groupoid. (Note that the same relationship does not hold between monoids and categories.)
Let $mathbf{C}$ denote a category. Then the isomorphisms of $mathbf{C}$ form a groupoid called the core of $mathbf{C}$, typically denoted $mathrm{core}(mathbf{C}).$ Now consider the automorphism function $mathrm{Aut}_mathbf{C} : mathrm{Obj}(mathbf{C}) rightarrow mathbf{Grp}$ that takes any object $X$ of $mathbf{C}$ to its group of automorphisms $mathrm{Aut}_mathbf{C}(X).$ This cannot be regarded as a functor out of $mathbf{C}$ in any sensible way. However, it can be regarded as a functor out of $mathrm{core}(mathbf{C})$.
The action of a group $G$ on a set (a "$G$-set") is precisely an object of the functor category
$[G,mathbf{Set}].$ More generally, the action of a group $G$ on a
"foo" is just an object of $[G,mathbf{Foo}]$, where $mathbf{Foo}$
is the category of foos. This makes sense even if $G$ is allowed to
be a general groupoid, or even a general category.
This explains why every homomorphism $varphi : G rightarrow H$ of groups gives rise to a functor $[H,mathbf{Set}] rightarrow [G,mathbf{Set}]$ "going the other way"; its because $mathrm{Hom}$ is contravariant in its first argument.
We may consider group objects in any category with finite products (note that we don't even need finite limits; finite products will do). For example, the group objects in $mathbf{Top}$ (the category of topological spaces) are precisely the topological groups.
Given a monoid $M$, every $M$-set $X$ is associated with a category $tilde{X}$ called its "translation category," defined as follows. The object set of $tilde{X}$ is just the underlying set of $X$. Given objects $x,y in X$, we define that an arrow $x rightarrow y$ is just a pair $(x,m)$ such that $m in M$ and $mx = y$. Composition of arrows is by multiplication. Explicitly:
$$(x,m_y)(y,m_z) = (x,m_z m_y).$$
Furthermore, if $G$ is a group and $X$ is a $G$-set, then the translation category $tilde{X}$ of $X$ is always a groupoid, called the translation groupoid of $X.$ Note also that every monoid acts on itself by left-multiplication. So given a monoid $M$, we may think of $M$ as an $M$-set, and hence we may write $tilde{M}$ and speak of the translation category of $M$. As a special case, if $G$ is a group, we may write $tilde{G}$ and speak of the translation groupoid of $G$.
For something a little more advanced, George Bergman has recently shown how to define the concepts of "inner automorphism" and "inner endomorphism" for objects of an arbitrary category. This could be an interesting viewpoint to take in your own report.
edited Dec 27 '15 at 18:00
answered Jan 9 '15 at 13:20
goblingoblin
37.1k1159193
37.1k1159193
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
add a comment |
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
You could add to item 5 that the functor from [H,Set] to [G,Set] has adjoints on both sides (Kan extensions).
$endgroup$
– Andreas Blass
Jan 9 '15 at 19:37
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
@AndreasBlass, interesting point. I know almost nothing about Kan extensions; how do we know they exist in this case?
$endgroup$
– goblin
Jan 10 '15 at 7:03
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
$begingroup$
I think the existence of the Kan extensions, for categories of functors into Set, is always true if the domain categories (in this case G and H) are small. But instead of quoting general results, one can also construct these adjoints explicitly in the case at hand.
$endgroup$
– Andreas Blass
Jan 10 '15 at 14:53
add a comment |
$begingroup$
You may want to look at Paolo Aluffi's book called Algebra Chapter zero. He begins talking about categories first and then introduces groups. He says a group is a groupoid (category in which every morphism is invertible) with only one object.
$endgroup$
add a comment |
$begingroup$
You may want to look at Paolo Aluffi's book called Algebra Chapter zero. He begins talking about categories first and then introduces groups. He says a group is a groupoid (category in which every morphism is invertible) with only one object.
$endgroup$
add a comment |
$begingroup$
You may want to look at Paolo Aluffi's book called Algebra Chapter zero. He begins talking about categories first and then introduces groups. He says a group is a groupoid (category in which every morphism is invertible) with only one object.
$endgroup$
You may want to look at Paolo Aluffi's book called Algebra Chapter zero. He begins talking about categories first and then introduces groups. He says a group is a groupoid (category in which every morphism is invertible) with only one object.
answered Jan 9 '15 at 15:23
Jorge Fernández HidalgoJorge Fernández Hidalgo
76.9k1394195
76.9k1394195
add a comment |
add a comment |
$begingroup$
On the [sub]topic of bibliography, there is a reasonable chapter (#4) in Steve Awodey's Category Theory book; the chapter introduces group theory with the help of category theory. Awodey is a philosophy prof at CMU, which probably explains why he put such a chapter in his book; the target audience isn't assumed have first learned group theory as the math undergrads normally do. A version of that chapter (probalby the one that appeared in the first edition of the book) is freely available on a CMU class webpage.
$endgroup$
add a comment |
$begingroup$
On the [sub]topic of bibliography, there is a reasonable chapter (#4) in Steve Awodey's Category Theory book; the chapter introduces group theory with the help of category theory. Awodey is a philosophy prof at CMU, which probably explains why he put such a chapter in his book; the target audience isn't assumed have first learned group theory as the math undergrads normally do. A version of that chapter (probalby the one that appeared in the first edition of the book) is freely available on a CMU class webpage.
$endgroup$
add a comment |
$begingroup$
On the [sub]topic of bibliography, there is a reasonable chapter (#4) in Steve Awodey's Category Theory book; the chapter introduces group theory with the help of category theory. Awodey is a philosophy prof at CMU, which probably explains why he put such a chapter in his book; the target audience isn't assumed have first learned group theory as the math undergrads normally do. A version of that chapter (probalby the one that appeared in the first edition of the book) is freely available on a CMU class webpage.
$endgroup$
On the [sub]topic of bibliography, there is a reasonable chapter (#4) in Steve Awodey's Category Theory book; the chapter introduces group theory with the help of category theory. Awodey is a philosophy prof at CMU, which probably explains why he put such a chapter in his book; the target audience isn't assumed have first learned group theory as the math undergrads normally do. A version of that chapter (probalby the one that appeared in the first edition of the book) is freely available on a CMU class webpage.
edited Jan 9 '15 at 21:55
answered Jan 9 '15 at 14:49
FizzFizz
1,636725
1,636725
add a comment |
add a comment |
$begingroup$
There are two books which link category theory and group theory via the use of groupoids. A pioneer in this was Philip Higgins, whose 1971 van Nostrand Notes are now available as free download as Categories and Groupoids (T&G). Following Philip's lead I started investigating groupoids in $1$-dimensional homotopy theory in 1965, and concluded that the groupoid point of view made many things clearer. The book I published in 1968 is now in its third edition and available as Topology and Groupoids. A key tool was the fundamental groupoid $pi_1(X,A)$ on a set $A$ of base points, chosen according to the geometry, which dates from 1967. The above are the only undergraduate texts in English using this concept. here is a mathoverview discussion on many base points, and a presentation on the background in algebraic topology was given at Galway in December, 2014. See also my preprint page.
A feature of both of these books is the use of the following construction. Let $G$ be a groupoid with object set $X$ and let $f:X to Y$ be a function to a set $Y$. Then we obtain a new groupoid which can be written $U_f(G)$ with object set $Y$ and a nice universal property. From this can be deduced the construction of coproducts of groups, and of free groups and free groupoids. This goes a long way to covering point 2 of @goblin's comment. Thus there is a combinatorial groupoid theory which in principle includes combinatorial group theory.
January 23, 2017 I should say that "combinatorial groupoid theory" is my own coinage, but also reflects JHC Whitehead's term "combinatorial homotopy theory".
The areas include those mentioned above and also fibrations and covering morphisms, groups acting on groupoids, (see T&G for all these). Other references are in my groupoids web page.

To answer the comment of goblin: how does one obtain a groupoid from a bundle of groups? The latter can be seen as a disjoint family ${G_s: s in S}$ of groups.
The associated groupoid $G$ has object set $S$ and a group $G_s$ for each $S in S$, so that $G(s,t)$ is empty if $s ne t$.
Another feature of the category of groupoids is the variety of morphisms. For groups there are mainly two special kinds of morphisms: injective or surjective. For groupoids we also have fibrations, covering morphisms, universal morphisms, orbit morphisms.
There is a special groupoid $mathcal I$ which has two objects $0,1$ and only one non identity $iota: 0 to 1$, and so also only $iota^{-1}: 1 to 0$. This seems a completely useless kind of object! But it defines a homotopy theory for groupoids, and also plays the same role in the category of groupoids as does the integers $ mathbf Z$ in the category of groups. Further, identifying $0,1$ in $mathcal I$ in the category of groupoids gives the integers $mathbf Z$, which explains the fundamental group of the circle!
$endgroup$
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
add a comment |
$begingroup$
There are two books which link category theory and group theory via the use of groupoids. A pioneer in this was Philip Higgins, whose 1971 van Nostrand Notes are now available as free download as Categories and Groupoids (T&G). Following Philip's lead I started investigating groupoids in $1$-dimensional homotopy theory in 1965, and concluded that the groupoid point of view made many things clearer. The book I published in 1968 is now in its third edition and available as Topology and Groupoids. A key tool was the fundamental groupoid $pi_1(X,A)$ on a set $A$ of base points, chosen according to the geometry, which dates from 1967. The above are the only undergraduate texts in English using this concept. here is a mathoverview discussion on many base points, and a presentation on the background in algebraic topology was given at Galway in December, 2014. See also my preprint page.
A feature of both of these books is the use of the following construction. Let $G$ be a groupoid with object set $X$ and let $f:X to Y$ be a function to a set $Y$. Then we obtain a new groupoid which can be written $U_f(G)$ with object set $Y$ and a nice universal property. From this can be deduced the construction of coproducts of groups, and of free groups and free groupoids. This goes a long way to covering point 2 of @goblin's comment. Thus there is a combinatorial groupoid theory which in principle includes combinatorial group theory.
January 23, 2017 I should say that "combinatorial groupoid theory" is my own coinage, but also reflects JHC Whitehead's term "combinatorial homotopy theory".
The areas include those mentioned above and also fibrations and covering morphisms, groups acting on groupoids, (see T&G for all these). Other references are in my groupoids web page.

To answer the comment of goblin: how does one obtain a groupoid from a bundle of groups? The latter can be seen as a disjoint family ${G_s: s in S}$ of groups.
The associated groupoid $G$ has object set $S$ and a group $G_s$ for each $S in S$, so that $G(s,t)$ is empty if $s ne t$.
Another feature of the category of groupoids is the variety of morphisms. For groups there are mainly two special kinds of morphisms: injective or surjective. For groupoids we also have fibrations, covering morphisms, universal morphisms, orbit morphisms.
There is a special groupoid $mathcal I$ which has two objects $0,1$ and only one non identity $iota: 0 to 1$, and so also only $iota^{-1}: 1 to 0$. This seems a completely useless kind of object! But it defines a homotopy theory for groupoids, and also plays the same role in the category of groupoids as does the integers $ mathbf Z$ in the category of groups. Further, identifying $0,1$ in $mathcal I$ in the category of groupoids gives the integers $mathbf Z$, which explains the fundamental group of the circle!
$endgroup$
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
add a comment |
$begingroup$
There are two books which link category theory and group theory via the use of groupoids. A pioneer in this was Philip Higgins, whose 1971 van Nostrand Notes are now available as free download as Categories and Groupoids (T&G). Following Philip's lead I started investigating groupoids in $1$-dimensional homotopy theory in 1965, and concluded that the groupoid point of view made many things clearer. The book I published in 1968 is now in its third edition and available as Topology and Groupoids. A key tool was the fundamental groupoid $pi_1(X,A)$ on a set $A$ of base points, chosen according to the geometry, which dates from 1967. The above are the only undergraduate texts in English using this concept. here is a mathoverview discussion on many base points, and a presentation on the background in algebraic topology was given at Galway in December, 2014. See also my preprint page.
A feature of both of these books is the use of the following construction. Let $G$ be a groupoid with object set $X$ and let $f:X to Y$ be a function to a set $Y$. Then we obtain a new groupoid which can be written $U_f(G)$ with object set $Y$ and a nice universal property. From this can be deduced the construction of coproducts of groups, and of free groups and free groupoids. This goes a long way to covering point 2 of @goblin's comment. Thus there is a combinatorial groupoid theory which in principle includes combinatorial group theory.
January 23, 2017 I should say that "combinatorial groupoid theory" is my own coinage, but also reflects JHC Whitehead's term "combinatorial homotopy theory".
The areas include those mentioned above and also fibrations and covering morphisms, groups acting on groupoids, (see T&G for all these). Other references are in my groupoids web page.

To answer the comment of goblin: how does one obtain a groupoid from a bundle of groups? The latter can be seen as a disjoint family ${G_s: s in S}$ of groups.
The associated groupoid $G$ has object set $S$ and a group $G_s$ for each $S in S$, so that $G(s,t)$ is empty if $s ne t$.
Another feature of the category of groupoids is the variety of morphisms. For groups there are mainly two special kinds of morphisms: injective or surjective. For groupoids we also have fibrations, covering morphisms, universal morphisms, orbit morphisms.
There is a special groupoid $mathcal I$ which has two objects $0,1$ and only one non identity $iota: 0 to 1$, and so also only $iota^{-1}: 1 to 0$. This seems a completely useless kind of object! But it defines a homotopy theory for groupoids, and also plays the same role in the category of groupoids as does the integers $ mathbf Z$ in the category of groups. Further, identifying $0,1$ in $mathcal I$ in the category of groupoids gives the integers $mathbf Z$, which explains the fundamental group of the circle!
$endgroup$
There are two books which link category theory and group theory via the use of groupoids. A pioneer in this was Philip Higgins, whose 1971 van Nostrand Notes are now available as free download as Categories and Groupoids (T&G). Following Philip's lead I started investigating groupoids in $1$-dimensional homotopy theory in 1965, and concluded that the groupoid point of view made many things clearer. The book I published in 1968 is now in its third edition and available as Topology and Groupoids. A key tool was the fundamental groupoid $pi_1(X,A)$ on a set $A$ of base points, chosen according to the geometry, which dates from 1967. The above are the only undergraduate texts in English using this concept. here is a mathoverview discussion on many base points, and a presentation on the background in algebraic topology was given at Galway in December, 2014. See also my preprint page.
A feature of both of these books is the use of the following construction. Let $G$ be a groupoid with object set $X$ and let $f:X to Y$ be a function to a set $Y$. Then we obtain a new groupoid which can be written $U_f(G)$ with object set $Y$ and a nice universal property. From this can be deduced the construction of coproducts of groups, and of free groups and free groupoids. This goes a long way to covering point 2 of @goblin's comment. Thus there is a combinatorial groupoid theory which in principle includes combinatorial group theory.
January 23, 2017 I should say that "combinatorial groupoid theory" is my own coinage, but also reflects JHC Whitehead's term "combinatorial homotopy theory".
The areas include those mentioned above and also fibrations and covering morphisms, groups acting on groupoids, (see T&G for all these). Other references are in my groupoids web page.

To answer the comment of goblin: how does one obtain a groupoid from a bundle of groups? The latter can be seen as a disjoint family ${G_s: s in S}$ of groups.
The associated groupoid $G$ has object set $S$ and a group $G_s$ for each $S in S$, so that $G(s,t)$ is empty if $s ne t$.
Another feature of the category of groupoids is the variety of morphisms. For groups there are mainly two special kinds of morphisms: injective or surjective. For groupoids we also have fibrations, covering morphisms, universal morphisms, orbit morphisms.
There is a special groupoid $mathcal I$ which has two objects $0,1$ and only one non identity $iota: 0 to 1$, and so also only $iota^{-1}: 1 to 0$. This seems a completely useless kind of object! But it defines a homotopy theory for groupoids, and also plays the same role in the category of groupoids as does the integers $ mathbf Z$ in the category of groups. Further, identifying $0,1$ in $mathcal I$ in the category of groupoids gives the integers $mathbf Z$, which explains the fundamental group of the circle!
edited Dec 21 '18 at 16:02
answered Mar 26 '15 at 22:02
Ronnie BrownRonnie Brown
12.1k12939
12.1k12939
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
add a comment |
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Do you know any good sources on combinatorial groupoid theory? (Papers are fine)
$endgroup$
– Paul Plummer
Mar 28 '15 at 20:47
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Look also at arXiv:1207.6404
$endgroup$
– Ronnie Brown
Apr 4 '15 at 21:50
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
$begingroup$
Amateur question: How does one obtain a groupoid from a bundle of groups?
$endgroup$
– goblin
Dec 14 '18 at 11:40
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f1097654%2fgroup-theory-via-category-theory%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
$begingroup$
Quite an odd hypothetical person - I imagine most people who know category theory studied abstract algebra before it.
$endgroup$
– rlms
Jan 9 '15 at 20:51
6
$begingroup$
@sweeneyrod, many people find themselves needing to revise abstract algebra "essentially from the beginning" though, despite knowing more advanced material.
$endgroup$
– goblin
Jan 10 '15 at 3:47
$begingroup$
@sweeneyrod, Maybe (finally!) category theory is coming first (possibly via computer science)
$endgroup$
– Jérôme JEAN-CHARLES
Aug 10 '15 at 13:48
$begingroup$
I think you'll find An Invitation to General Algebra and Universal Constructions useful. The title should make the reason obvious.
$endgroup$
– M. Vinay
Jan 22 '16 at 3:55
$begingroup$
@sweeneyrod Well, it is not hypothetical. I am an example. I learned about limits and adjunctions before learning, what a centralizer is.
$endgroup$
– Stefan Perko
Jan 23 '17 at 21:47