Vrftsjtryk

Termodinâmica
Processo de convecção.
Glossário de termodinâmica
Ramos Clássica Estatística Química
Leis Zero Primeira Segunda Terceira
Sistema termodinâmico Sistema termodinâmico Estado Equação de estado Gás ideal Gás real Estados físicos da matéria Equilíbrio Volume de controle Transformações Transformação termodinâmica Isobárica Isocórica Isotérmica Adiabática Isentrópica Isentálpica Politrópica Expansão livre Reversibilidade Irreversibilidade Ciclos Ciclo termodinâmico Máquinas térmicas Ciclo de refrigeração Eficiência termodinâmica
Grandezas físicas Funções de estado Nota: Variáveis conjugadas em itálico Propriedades extensivas e intensivas Calor Calor específico Condutividade térmica Densidade Energia Entropia Fluxo Potência Potencial químico Pressão Temperatura Título Trabalho Vazão Volume
Propriedades Capacidade térmica específica  c={displaystyle c=} T{displaystyle T} ∂S{displaystyle partial S} N{displaystyle N} ∂T{displaystyle partial T} Compressibilidade  β=−{displaystyle beta =-} 1{displaystyle 1} ∂V{displaystyle partial V} V{displaystyle V} ∂p{displaystyle partial p} Dilatação térmica  α={displaystyle alpha =} 1{displaystyle 1} ∂V{displaystyle partial V} V{displaystyle V} ∂T{displaystyle partial T}
Equações termodinâmicas Teorema de Carnot Lei dos gases ideais Relações de Maxwell Teorema da equipartição Teorema do virial Lei de Henry Lei de Boyle-Mariotte Equação de Van der Waals Raio de Van der Waals Lei de Charles
Potencial termodinâmico Potencial termodinâmico Energia livre Energia interna U(S,V){displaystyle U(S,V)} Entalpia H(S,p)=U+pV{displaystyle H(S,p)=U+pV} Energia livre de Helmholtz A(T,V)=U−TS{displaystyle A(T,V)=U-TS} Energia livre de Gibbs G(T,p)=H−TS{displaystyle G(T,p)=H-TS}
História Cultura História Geral Leis dos gases Filosofia Demônio de Maxwell Teorias Teoria calórica Teoria do calor Vis viva ("força viva") Equivalente mecânico do calor Potência motriz
Cientistas Bernoulli Boltzmann Carnot Clapeyron Clausius Carathéodory Duhem Gibbs von Helmholtz Joule Maxwell von Mayer Onsager Rankine Smeaton Stahl Thompson Thomson van der Waals Waterston
v d e

A termodinâmica (do grego θερμη, therme, significa "calor"^{[Ref. 1]}e δυναμις, dynamis, significa "potência") é o ramo da física que estuda as causas e os efeitos de mudanças na temperatura, pressão e volume — e de outras grandezas termodinâmicas fundamentais em casos menos gerais — em sistemas físicos em escala macroscópica. Grosso modo, calor significa "energia" em trânsito, e dinâmica se relaciona com "movimento". Por isso, em essência, a termodinâmica estuda o movimento da energia e como a energia cria movimento. Historicamente, a termodinâmica se desenvolveu pela necessidade de aumentar a eficiência das primeiras máquinas a vapor,^{[Ref. 2]}sendo em essência uma ciência experimental, que diz respeito apenas a propriedades macroscópicas ou de grande escala da matéria e energia.^{[Ref. 3]}

Considerações históricas |

Pessoas importantes na história da termodinâmica.^[1]

Linha de tempo de pessoas importantes para a termodinâmica.

O wikilivro História e epistemologia da Física tem uma página intitulada A Ciência na Grécia

A breve história da termodinâmica começa com Guericke, que em 1650 projetou e construiu a primeira bomba de vácuo do mundo, e o primeiro vácuo artificial do mundo, através dos hemisférios de Magdeburgo. Ele foi incentivado pela busca em provar a invalidade da antiga percepção de que "a natureza tem horror ao vácuo" e de que não poderia haver vazio ou vácuo, "pois no vácuo todos os corpos cairiam com a mesma velocidade" tal como descreveu em ambos os casos Aristóteles.

Logo após este evento, o físico e químico irlandês Robert Boyle tomou ciência dos experimentos de Guericke, e em 1656, em coordenação com o cientista inglês Robert Hooke, construiu uma bomba de ar.^{[Ref. 4]}Usando esta bomba, Boyle e Hooke perceberam uma correlação entre pressão, temperatura e volume. Com isso foi formulada a Lei de Boyle, a qual estabelece que a pressão e o volume são inversamente proporcionais. Então, em 1679, baseado nestes conceitos, um conhecido de Boyle chamado Denis Papin construiu um forno de pressão (marmita de Papin), que era um vaso fechado com uma tampa fechada hermeticamente que confinava o vapor até alta pressão ser gerada.

Projetos posteriores incluíram uma válvula de alívio para o vapor, evitando que o recipiente explodisse devido à alta pressão. Observando o movimento rítmico da válvula de alívio para cima e para baixo, Papin concebeu a ideia de uma máquina constituída de um pistão e um cilindro. Mas Papin não seguiu adiante com a ideia. Foi somente em 1697, baseado nas ideias de Papin, que o engenheiro Thomas Savery construiu a primeira máquina a vapor. Embora nesta época as máquinas fossem brutas e ineficientes, elas atraíram a atenção dos principais cientistas da época. Um destes cientistas foi Sadi Carnot, o "pai da termodinâmica", que em 1824 publicou "Reflexões sobre a Potência Motriz do Fogo", um discurso sobre o calor, potência e eficiência de máquina. O texto trouxe as relações energéticas básicas entre a máquina de Carnot, o ciclo de Carnot e a potência motriz. Isto marcou o início da termodinâmica como ciência moderna.^{[Ref. 5]}

Algumas ideias relevantes |

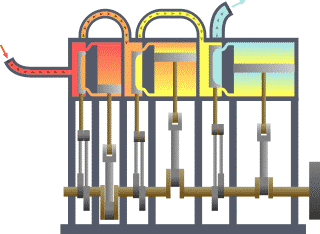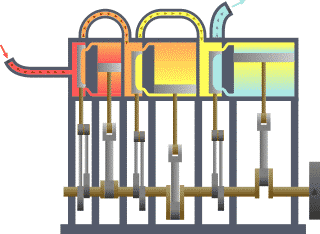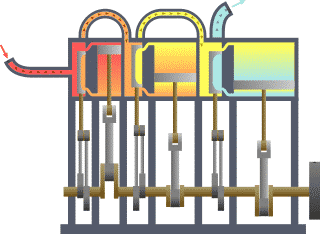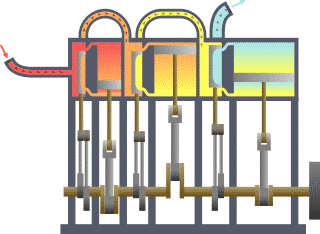
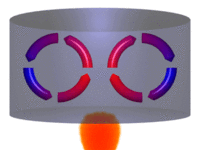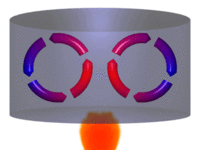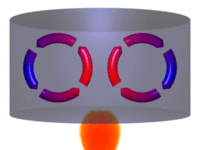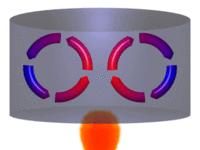
Diagrama de um sistema termodinâmico típico: uma máquina térmica cíclica. Parte da energia admitida — oriunda de uma fonte quente (em vermelho, à esquerda) — é convertida em trabalho (movimento), neste caso por uma série de pistões. Contudo, em máquinas cíclicas não se pode converter toda a energia oriunda da fonte quente em trabalho, havendo necessariamente uma quantidade mínima de energia rejeitada a uma fonte fria (em azul, à direita).

É bastante conhecido o fato de que qualquer porção de matéria ou determinada substância é constituída por um número muito grande de partículas microscópicas fundamentais - átomos ou moléculas conforme o caso, em geral, ou outrem, em casos mais específicos.^{[Nota 1]}Embora a termodinâmica utilize - quando disponíveis - as propriedades microscópicas de um sistema de partículas para inferir suas propriedades macroscópicas, a termodinâmica não descreve as propriedades microscópicas deste. As propriedades termodinâmicas deste sistema de partículas são determinadas apenas por suas propriedades macroscópicas.

Partindo de um ponto de vista puramente macroscópico para o estudo do sistema - que não requer o conhecimento do comportamento individual das partículas microscópicas que integram o mesmo - desenvolveu-se a chamada termodinâmica clássica. Ela permite abordar de uma maneira fácil e direta os problemas correlatos ao comportamento da matéria e energia em tal escala e as soluções para os mesmos. Uma abordagem mais elaborada, baseada no comportamento médio de grandes grupos de partículas, é chamada de termodinâmica estatística.^{[Ref. 5][Ref. 6]} A termodinâmica estatística trouxe respostas, entre outros, quanto à natureza de conceitos como energia interna e temperatura associados aos sistemas termodinâmicos, e neste âmbito, a termodinâmica pode ser definida como a área de estudos que descreve e analisa o comportamento macroscópico de sistemas constituídos por um número de partículas e necessariamente alto - no limite termodinâmico, "infinito" - para inviabilizar a análise prática do mesmo mediante a análise individual de cada partícula que o compõe.

O ponto inicial para a maioria das considerações termodinâmicas são as leis da termodinâmica, que postulam as características intrínsecas a todo sistema termodinâmico, e também que a energia pode ser transferida de um sistema físico para outro como calor ou trabalho.^{[Nota 2][Ref. 7]}Elas também postulam a existência de uma quantidade chamada entropia, que pode ser definida para qualquer sistema.^{[Ref. 8]}

Em termodinâmica, interações entre sistemas são particularmente enfocadas, estudadas e categorizadas. Para este estudo, os conceitos de sistema e vizinhanças são centrais — e por tal também são de extrema relevância as características das fronteiras que os definem. Um sistema termodinâmico é composto de "infinitas" partículas encerradas dentro de uma fronteira, cujos movimento e inter-relacionamento médios ou totais definem suas propriedades termodinâmicas, cujas relações são expressas através de equações de estado, sendo estas certamente de vital relevância ao estudo termodinâmico de tais sistemas. Tais propriedades podem também ser adequadamente combinadas de forma a expressar a energia interna ou os demais potenciais termodinâmicos — ou a entropia e suas transformadas — como equações fundamentais — que são extremamente úteis na compreensão e análise das condições de equilíbrio e em processos ou transformações, espontâneos ou não, associados ao sistema. Uma equação fundamental, ao contrário de uma equação de estado, sempre encerra em si todas as informações termodinâmicas do sistema à qual se associa. Ao conjunto de todos os sistemas com o quais o sistema em foco se relaciona através de fronteiras comuns dá-se o nome de vizinhança. Ao conjunto de todos os sistemas pertinentes dá-se o nome de universo.

Com suas ferramentas — o formalismo da termodinâmica — a termodinâmica descreve não apenas os sistemas, mas também como os sistemas respondem a mudanças em sua vizinhança. Isso pode ser aplicado a uma ampla variedade de tópicos em ciência e tecnologia, como por exemplo, máquinas, transições de fases, reações químicas, fenômenos de transporte e até buracos negros. Os resultados da termodinâmica são essenciais para outros campos da física e da química, engenharia química, engenharia aeroespacial, engenharia mecânica, biologia celular, engenharia biomédica, engenharia ferroviária, ciências dos materiais e economia, para citar alguns.^{[Ref. 9][Ref. 10]}

Transformações e processos |

Existem dois tipos fundamentais de entidade em termodinâmica, estados de um sistema, e os processos de um sistema. Isto permite três abordagens fundamentais para raciocínio termodinâmico: em termos de estados de equilíbrio termodinâmico do sistema, em termos de processos invariantes no tempo de um sistema, e em termos de processos cíclicos de um sistema.

Sempre que duas^{[Nota 3]}ou mais propriedades de um sistema variam, diz-se que ocorreu um processo. Sempre que há mudança entre estados de equilíbrio há um processo. Um processo é geralmente descrito por um diagrama identificando os sucessivos estados pelo qual passa o sistema durante o transcurso do mesmo. Um processo de quase-equilíbrio (quase-estático) é aquele em que o desvio do equilíbrio termodinâmico ao ir-se de um estado de equilíbrio ao subsequente é infinitesimal, de forma que o sistema pode ser considerado a qualquer momento como estando em um dos estados de equilíbrio. Assim um processo quase estático se aproxima muito de uma sucessão de estados de equilíbrio, e tais processos têm diagramas representativos descritos por linhas, e não por pontos não intercalados, em um diagrama de estados.^{[Ref. 3]}Muitos processos reais, geralmente os processos lentos, podem ser considerados com razoável precisão como sendo processos de quase-equilíbrio. Vários outros - entre os quais os processos que ocorrem de forma brusca - não.
O termo "transformação" é normalmente utilizado para referenciar um processo quase-estático.

Abordagem e exemplos |

A abordagem através de estados de equilíbrio termodinâmico do sistema requer um relato completo do estado do sistema, bem como a noção de processo a partir de um estado para outro de um sistema, mas pode necessitar de apenas uma conta idealizada ou parcial, do estado do entorno do sistema ou de outros sistemas.
O método de descrição em termos de estados de equilíbrio termodinâmico tem limitações. Por exemplo, os processos em uma região de fluxo turbulento, ou numa mistura de gás de queima, ou de um gás pode ser além Knudsen "da província de termodinâmica".^[2][3][4] Este problema pode ser contornado por vezes através do método da descrição, em termos de processos cíclicos ou de tempo invariantes de fluxo. Esta é parte da razão pela qual os fundadores da termodinâmica muitas vezes preferiram a descrição do processo cíclico.

Aproximações através de processos de invariante no tempo de fluxo de um sistema são utilizadas para alguns estudos. Alguns processos, por exemplo, a expansão de Joule-Thomson, são estudados por meio de fluxo estacionário de experiências, mas pode ser explicado por distinguir a energia cinética do fluxo contínuo a granel a partir da energia interna e, assim, podem ser consideradas como dentro do âmbito da termodinâmica clássica definidos em termos de estados de equilíbrio ou de processos cíclicos.^[5] Outros processos de fluxo, por exemplo, efeitos termoelétricos, são essencialmente definidos pela presença de fluxos diferenciais ou de difusão de modo que eles não podem ser adequadamente avaliados em termos de estados de equilíbrio ou processos cíclicos clássicos..^[6][7]

A noção de um processo cíclico não requer uma conta completa do estado do sistema, mas requer um relato completo de como ocasiões em que o processo de transferências de matéria e energia entre o sistema principal (que é muitas vezes chamado de corpo de trabalho) e sua ambiente, devem incluir, pelo menos, dois reservatórios de calor em diferentes temperaturas conhecidas e fixas, uma temperatura superior a do sistema principal e uma mais fria do que o outro, assim como um reservatório, que pode receber a energia do sistema como o trabalho e pode fazer o trabalho do sistema. Os reservatórios podem, alternativamente, ser considerados como sistemas de componentes auxiliares idealizados, a par do sistema principal. Assim, uma consideração em termos de processos cíclicos requer pelo menos quatro sistemas de componentes contributivos. As variáveis independentes desta conta são as quantidades de energia que entram e saem dos sistemas idealizados auxiliares. Neste tipo de conta, o corpo de trabalho é muitas vezes considerado como uma "caixa preta",^[8] e seu próprio estado não é especificado. Nesta abordagem, a noção de uma escala numérica de temperatura adequada empírica é um pressuposto da termodinâmica, e não uma noção construída por ela ou derivados dela.

Conta em termos de estados de equilíbrio termodinâmico |

Quando o sistema está em equilíbrio termodinâmico sob um dado conjunto de condições do seu ambiente, diz-se estar num estado termodinâmico definido, que é completamente descrito por variáveis de estado.
Se um sistema é muito simples, tal como definido acima, e está em equilíbrio termodinâmico, e não está sujeito a um campo de força aplicada externamente, tal como a gravidade, a eletricidade ou o magnetismo, então é homogênea, isto é, digamos, espacialmente uniforme em todos os aspectos.^[9]
De certo modo, um sistema homogêneo pode ser considerado como espacialmente zero-dimensional, porque ele não tem a variação espacial.
Se um sistema em equilíbrio termodinâmico é homogêneo, em seguida, o seu estado pode ser descrito por algumas variáveis físicas, que são na sua maioria classificadas como variáveis intensivas e variáveis extensivas.^[10][11]

Exemplos |

Exemplos de variáveis termodinâmicas extensivas são massa total e volume total. Exemplos de variáveis termodinâmicas intensivas são a temperatura, pressão e concentração de produtos químicos; variáveis termodinâmicas intensivas são definidas em cada ponto espacial e cada instante de tempo em um sistema. Variáveis físicas macroscópicas podem ser mecânicas ou térmicas. A temperatura é uma variável térmica, Segundo Guggenheim, " Concepção mais importante é a temperatura termodinâmica".
Variáveis intensivas são definidas pela propriedade de que, se qualquer número de sistemas, cada um no seu estado de equilíbrio termodinâmico separado homogêneo, todos com os mesmos valores respectivos de todas as suas variáveis intensivas, independentemente dos valores de suas variáveis extensivas, são dispostas de forma contígua com a partição entre eles, de modo a formar um novo sistema, em seguida, os valores das variáveis de intensidade do novo sistema são os mesmos que os dos sistemas de componentes separadas. Tal sistema é composto de um equilíbrio termodinâmico homogêneo. Exemplos de variáveis intensivas são a temperatura, a concentração química, pressão, densidade de massa, a densidade de energia interna, e, quando pode ser adequadamente definido densidade de entropia.^[12]

Definições de variáveis |

Variáveis extensivas são definidas pela propriedade de que, se qualquer número de sistemas, independentemente do seu equilíbrio termodinâmico possível separado ou estados de não-equilíbrio ou variáveis intensivas, são dispostos lado a lado com a partição entre eles de modo a formar um novo sistema, em seguida, os valores das variáveis de largo espectro do novo sistema são as somas dos valores das variáveis respectivas extensivas dos sistemas individuais constituintes separados. Obviamente, não há nenhuma razão para esperar que um tal sistema composto estar em equilíbrio termodinâmico homogêneo. Exemplos de variáveis extensivas são massa, volume e energia interna. Eles dependem da quantidade total de massa no sistema.^[13]
Porém, quando ela pode ser adequadamente definida, a densidade de entropia é uma variável intensiva. Para sistemas heterogêneos, a entropia em si não se encaixa nesta classificação de variáveis de estado.^[14][15] A razão é que a entropia é uma propriedade de um sistema como um todo, e não necessariamente relacionada simplesmente aos seus constituintes separadamente. Para qualquer número de sistemas e cada um no seu próprio equilíbrio termodinâmico separado homogêneo, todos com os mesmos valores de variáveis de intensidade, a remoção das divisórias entre os resultados distintos dos sistemas em um sistema composto homogêneo em equilíbrio termodinâmico, com todos os valores de suas variáveis intensivas (os mesmos que os dos sistemas constituintes), é reservadamente ou condicionalmente verdade que a entropia de um sistema desse tipo definido, de forma restritiva, composto, é a soma das entropias dos sistemas constituintes. Mas se os sistemas constituintes não satisfazem estas condições restritivas, a entropia de um sistema composto não pode ser esperada como sendo a soma das entropias dos sistemas constituintes, pois a entropia é uma propriedade do sistema composto como um todo. Portanto, ainda que sob estas reservas restritivas, a entropia satisfaz alguns requisitos para a extensividade definidos acima; a entropia, em geral, não se encaixa na definição acima de uma variável extensiva.

Não sendo nem uma variável intensiva nem uma variável extensiva de acordo com a definição acima, a entropia é uma variável de "stand-out", porque é uma variável de estado de um sistema como um todo.^[14] Um sistema de não-equilíbrio pode ter uma estrutura dinâmica não-homogênea. Esta é uma razão para distinguir o estudo da termodinâmica de equilíbrio a partir do estudo de não-equilíbrio termodinâmica.
A razão física para a existência de variáveis extensivas é o tempo de invariância de volume em um dado referencial inercial, e a conservação estritamente local de massa, força, momento angular e da energia. Como observado por Gibbs, a entropia é diferente de energia e massa, porque não é localmente conservada.^[14] A quantidade de entropia "stand-out" nunca se conserva em processos físicos reais. Todos os processos físicos reais são irreversíveis.^[16] O movimento dos planetas parece reversível em uma escala de tempo curta (milhões de anos), mas seu movimento, de acordo com as leis de Newton, é matematicamente um exemplo de caos determinístico. Eventualmente, um planeta sofre uma colisão com um objeto imprevisível do seu entorno, o espaço exterior, neste caso, e, consequentemente, o seu curso futuro é radicalmente imprevisível. Teoricamente, isso pode ser expresso dizendo que cada processo natural dissipa algumas informações da parte previsível da sua atividade para a parte imprevisível. A parte previsível é expressa nas variáveis generalizadas mecânicas, e na parte imprevisível em calor.

Outras variáveis |

Outras variáveis de estado podem ser consideradas como sujeitas condicionalmente "extensivas" a reserva acima, mas não extensivas como definido acima. Exemplos são a energia livre de Gibbs, a energia livre de Helmholtz, e a entalpia. Consequentemente, apenas porque para alguns sistemas sob condições particulares de seus arredores variáveis de estado sejam condicionalmente conjugar a variáveis intensivas, tal conjugação não faz variáveis de estado tais extensivas como definido acima. Esta é uma outra razão para distinguir o estudo da termodinâmica de equilíbrio a partir do estudo de não-equilíbrio termodinâmico. Numa outra forma de pensar, isto explica porque o calor deve ser considerado como uma quantidade que se refere a um processo, e não a um estado de um sistema.
Um sistema sem divisórias internas, e em equilíbrio termodinâmico, pode ser heterogêneo no respeito seguinte: pode consistir em várias "fases", cada uma homogênea em si, em contiguidade imediata com outras fases do sistema, mas distinguíveis por ter várias características físicas diferentes, respectivamente, com a interrupção do fluxo de variáveis intensivas nos limites entre as fases. Uma mistura de espécies químicas diferentes é considerado homogênea por este efeito, se é fisicamente homogênea.^[17] Por exemplo, um recipiente pode conter um sistema constituído por água líquida sobrejacente vapor e, depois, existe uma fase de vapor e uma fase líquida, cada uma homogênea em si mesma, mas ainda em equilíbrio termodinâmico com a outra fase. Para a conta imediatamente presente, sistemas com múltiplas fases não são considerados, embora por questões termodinâmicas muitos sistemas multifásicos são importantes.

Equação de estado |

As variáveis macroscópicas de um sistema termodinâmico em equilíbrio termodinâmico, em que a temperatura está bem definida, pode ser relacionado com um outro por meio de equações de equações de estado ou característica. E expressam as peculiaridades constitutivas o material do sistema. A equação de estado deve cumprir com algumas restrições termodinâmicas, mas não pode ser derivada a partir dos princípios gerais da termodinâmica sozinhos.^{[carece de fontes?]}

Os processos termodinâmicos entre os estados de equilíbrio termodinâmico |

Um processo termodinâmico é definido por mudanças de estado interno do sistema de interesse, juntamente com a transferência de matéria e de energia ao ambiente do sistema ou a outros sistemas. Um sistema é demarcado do seu ambiente ou de outros sistemas, por divisórias que mais ou menos separadas, podem mover-se como um êmbolo para alterar o volume do sistema e, portanto, transferir o trabalho.^{[carece de fontes?]}

As variáveis dependentes e independentes para um processo |

Um processo é descrito por mudanças nos valores das variáveis de estado dos sistemas ou por quantidades de troca de matéria e energia entre sistemas e ambientes. A mudança deve ser especificada em termos de variáveis prescritas. A escolha de quais variáveis que devem ser usadas é feita antes da análise do decurso do processo, e não pode ser alterada. Algumas das variáveis escolhidas com antecedência são chamadas de variáveis independentes.^[18] A partir de alterações em variáveis independentes podem ser derivadas mudanças em outras variáveis chamadas variáveis dependentes. Por exemplo, um processo pode ocorrer a uma pressão constante com pressão prescrita como uma variável independente, e temperatura alterada como uma outra variável independente, e, em seguida, as variações de volume são consideradas como dependentes. Atenção a este princípio, é necessário em termodinâmica.^[19][20]

Mudanças de estado de um sistema |

Mudanças de estado em um sistema.

Na abordagem através de estados de equilíbrio do sistema, um processo pode ser descrito em duas formas principais.
De certa forma, o sistema é considerado para ser ligado ao meio de algum tipo de partição de separação, e deixa-se atingir o equilíbrio com o ambiente, com a partição no seu lugar. Então, quando o caráter de separação da partição é mantido inalterado, as condições do meio são alteradas, e exercem a sua influência sobre o sistema novamente através da divisória de separação, ou a partição é deslocada de modo a alterar o volume do sistema; e um novo equilíbrio é atingido. Por exemplo, um sistema é deixado atingir o equilíbrio com um banho de aquecimento a uma temperatura, em seguida, a temperatura do banho de aquecimento é alterada e o sistema é deixado atingir um novo equilíbrio, se a partição permite a condução de calor, o novo equilíbrio é diferente do equilíbrio anterior.
De outro modo, vários sistemas estão ligados um ao outro por várias espécies de divisórias de separação, e para atingir o equilíbrio um com o outro, com as divisórias no lugar. Desta forma, pode-se falar de um "sistema composto". Em seguida, uma ou mais partições são removidas ou alteradas nas suas propriedades de separação ou são movidas, e um novo equilíbrio é atingido. O experimento de Joule-Thomson, é um exemplo deste, um tubo de gás é separado do outro por uma divisória de tubo poroso, o volume disponível em cada um dos tubos é determinado por meio de pistões respectivos; equilíbrio é estabelecido com um conjunto inicial de volumes; o volumes são alterados e um novo equilíbrio é estabelecido.^{[21][22][23][24][25]} Um outro exemplo é a separação e mistura de gases, com o uso de membranas quimicamente semi-permeáveis.^[26]

Os processos termodinâmicos comumente considerados |

É muitas vezes conveniente para estudar um processo termodinâmico, em que uma única variável, tal como a temperatura, a pressão ou o volume, etc, é mantido fixo. Além disso, é útil agrupar estes processos em pares, em que cada variável é mantida constante como um membro de um par conjugado.
Vários processos termodinâmicos comumente estudados são:

• 
  Processo isobárico: ocorre a pressão constante


• 
  Processo isocórico: ocorre a volume constante (também chamado isométrica / isovolumétrico)


• 
  Processo isotérmico: ocorre a uma temperatura constante


• 
  Processo adiabático: ocorre sem perda ou ganho de energia como calor
  


• 
  Processo isentrópico: um processo reversível adiabático ocorre a uma entropia constante, mas é uma idealização de ficção. Conceitualmente, é possível realizar fisicamente um processo que mantém a entropia do sistema constante, permitindo a remoção sistemática controlada de calor, por condução para um corpo mais frio, para compensar a entropia produzida dentro do sistema de trabalho feito irreversível no sistema. Tal conduta isentrópica de um processo chamado parece para quando a entropia do sistema é considerada como uma variável independente, por exemplo, quando a energia interna é considerada como uma função da entropia e volume do sistema, as variáveis naturais da energia interna como estudado por Gibbs.


• 
  Processo isentálpico: ocorre a uma entalpia constante


• 
  Processo isolado: nenhuma matéria ou energia (nem como trabalho nem na forma de calor) é transferido para dentro ou para fora do sistema

Por vezes, é de interesse para o estudo de um processo no qual uma série de variáveis são controladas, sujeitas a alguma restrição especificada. Num sistema em que uma reação química pode ocorrer, por exemplo, em que a pressão e a temperatura podem afetar a composição de equilíbrio, um processo pode ocorrer em que a temperatura é mantida constante, mas a pressão é lentamente alterada, de modo que apenas o equilíbrio químico é mantido a forma. Há um processo correspondente a uma temperatura constante em que a pressão final é a mesma, mas é atingida por um salto rápido. Em seguida, pode-se mostrar que a variação do volume resultante do processo de salto rápido é menor do que a partir do processo de equilíbrio lentos.^[27] O trabalho transferido difere entre os dois processos.

Conta em termos de processos cíclicos |

Um processo cíclico^[28] é um processo que pode ser repetido indefinidamente, muitas vezes, sem alterar o estado final do sistema no qual o processo ocorre. Os únicos vestígios dos efeitos de um processo cíclico são encontrados nas imediações do sistema ou em outros sistemas. Este é o tipo de processo que causa termodinamicistas precoces, como Carnot, e em termos dos quais Kelvin definiu temperatura absoluta,^[29][30] antes da utilização da quantidade de entropia por Rankine,^[31] e a sua identificação clara de Clausius.^[32] Para alguns sistemas, por exemplo, com algumas substâncias plásticas úteis, processos cíclicos são praticamente quase impraticáveis porque a substância de trabalho passa por mudanças praticamente irreversíveis. É por isso que os dispositivos mecânicos são lubrificados com o óleo e uma das razões pelas quais os dispositivos elétricos são muitas vezes úteis.
Um processo cíclico de um sistema requer a sua envolvente, pelo menos, dois reservatórios de calor, a temperaturas diferentes, um a uma temperatura mais elevada, que fornece calor para o sistema, o outro a uma temperatura mais baixa que aceita o calor do sistema. Os primeiros trabalhos sobre termodinâmica tendiam a usar a abordagem de processo cíclico, pois estavam interessados em máquinas que converteram parte do calor do entorno em potência mecânica entregue ao ambiente, sem muita preocupação sobre o funcionamento interno da máquina. Uma tal máquina, ao receber uma quantidade de calor a partir de um reservatório de temperatura mais elevada, necessita sempre de um reservatório de baixa temperatura que aceita uma menor quantidade de calor, a diferença na quantidade de calor que é convertido para o trabalho.^[33][34] Mais tarde, o funcionamento interno de um sistema tornou-se de interesse, e é descrito pelos estados do sistema. Hoje em dia, em vez de discutir em termos de processos cíclicos, alguns escritores são inclinados a derivar o conceito de temperatura absoluta do conceito de entropia, uma variável de estado.

Potenciais |

Potenciais termodinâmicos são diferentes medidas quantitativas da energia armazenada no sistema. Potenciais são usados para medir as mudanças de energia em sistemas como eles evoluem a partir de um estado inicial a um estado final. O potencial utilizado depende das limitações do sistema, tais como a temperatura ou a pressão constante. Por exemplo, as energias de Helmholtz e Gibbs são as energias disponíveis em um sistema para realizar trabalho útil, quando a temperatura e o volume ou a pressão e a temperatura são fixos, respectivamente.
Os cinco potenciais mais conhecidas são:

Nome	Símbolo	Fórmula	Variáveis
Energia interna	U{displaystyle U}	∫(TdS−pdV+∑iμidNi){displaystyle int (TdS-pdV+sum _{i}mu _{i}dN_{i})}	S,V,{Ni}{displaystyle S,V,{N_{i}}}
Energia Livre de Helmholtz	F,A{displaystyle F,,A}	U−TS{displaystyle U-TS}	T,V,{Ni}{displaystyle T,V,{N_{i}}}
Entalpia	H{displaystyle H}	U+pV{displaystyle U+pV}	S,p,{Ni}{displaystyle S,p,{N_{i}}}
Energia Livre de Gibbs	G{displaystyle G}	U+pV−TS{displaystyle U+pV-TS}	T,p,{Ni}{displaystyle T,p,{N_{i}}}
Potencial de Landau (Grand potential)	Ω,ΦG{displaystyle Omega ,,Phi _{G}}	U−TS−{displaystyle U-TS-}∑i{displaystyle sum _{i},}μiNi{displaystyle mu _{i}N_{i}}	T,V,{μi}{displaystyle T,V,{mu _{i}}}

T{displaystyle T} é a temperatura, S{displaystyle S} a entropia, p{displaystyle p} a pressão, V{displaystyle V} o volume, μ{displaystyle mu } o potencial químico, N{displaystyle N} o número de partículas no sistema, e i{displaystyle i} é a contagem de tipos de partículas no sistema.
Potenciais termodinâmicos podem ser derivados a partir da equação de equilíbrio de energia aplicada a um sistema termodinâmico. Outros potenciais termodinâmicos podem também ser obtidos através de transformação de Legendre.

Princípios da termodinâmica |

Princípio zero: entrando em equilíbrio |

O princípio básico sobre o qual a termodinâmica se assenta é^{[Nota 4]}: dado um sistema isolado - envolto por uma fronteira completamente restritiva em relação à troca de energia ou matéria - haverá um estado em particular, caracterizado pela constância de todas as grandezas termodinâmicas mensuráveis (temperatura, pressões parciais, volume das fases, etc.), que, uma vez dado tempo suficiente para as transformações necessárias ocorrerem, sempre será atingido. Os valores a serem assumidos pelas grandezas no estado de equilíbrio encontram-se univocamente determinados desde o estabelecimento da fronteira e do sistema, dependendo estes, em sistemas simples, apenas do número e natureza das partículas, do volume e da energia interna encerrados no sistema. Tal estado final de equilíbrio do sistema é nomeado estado de equilíbrio termodinâmico. A rigor define-se temperatura apenas para o estado de equilíbrio termodinâmico, não se definindo em princípio a mesma grandeza para sistemas fora do equilíbrio.

O princípio zero ainda engloba o raciocínio de que, se dois sistemas A e B - cada qual já em seu respectivo estado de equilíbrio - forem colocados um a um em contato de forma adequada com um sistema C, e verificar-se experimentalmente que estes mantiveram os respectivos estados de equilíbrio originais, estes estarão não apenas em equilíbrio com C mas também estarão em equilíbrio entre si, de forma que também manterão seus respectivos estados de equilíbrio originais se colocados em contato mediante fronteira semelhante. Considera-se para tal geralmente uma fronteira não restritiva apenas quanto à troca de calor, caso em que se fala em equilíbrio térmico . Tal princípio implica, pois: se a temperatura de A e B são iguais à de C, as temperaturas de A e B serão também necessariamente iguais. Se a fronteira não for restritiva quanto à troca de energia em qualquer de suas formas - calor ou trabalho - mas o for ainda em relação à troca de matéria, falar-se-á em equilíbrio térmico e mecânico. Neste caso, não somente suas temperaturas mas também suas pressões serão iguais. Se a fronteira for completamente irrestritiva, permitindo inclusive a troca de matéria e reações químicas, falar-se-á em equilíbrio térmico, mecânico e (eletro)químico, ou seja, em equilíbrio termodinâmico.^{[Ref. 3]}

Este princípio básico - conhecido por razões cronológicas e históricas como princípio zero da termodinâmica - é o que possibilita a definição macroscópica de temperatura e também a construção de termômetros.

Princípio primeiro: conservando a energia |

Observação: a compreensão do que se segue exige o conhecimento das definições de: energia, energia interna, energia térmica, temperatura (absoluta), energia potencial, pressão, volume, calor e trabalho. Solicita-se a leitura dos artigos específicos caso estes conceitos não se mostrem familiares.

De acordo com o princípio da Conservação da Energia, a energia não pode ser criada nem destruída, mas somente transformada de uma espécie em outra. O primeiro princípio da termodinâmica estabelece uma equivalência entre o trabalho e o calor trocados entre um sistema e seu meio exterior no que se refira à variação da energia interna do sistema.

Considere um sistema e sua vizinhança, em uma situação tal que uma certa quantidade de calor Q tenha atravessado a fronteira comum aos dois (devido à diferença de temperaturas entre ambos). Considere também que a fronteira comum entre os sistemas se mova neste processo, implicando em energia trocada na forma de trabalho entre ambos. Neste caso a variação na energia interna do sistema em foco é expressa por:

 ΔU=Q−W{displaystyle Delta U=Q-W}^{[Ref. 11][Ref. 3]}

A expressão acima representa analiticamente o primeiro princípio da termodinâmica, cujo enunciado pode ser:

" a variação da energia interna de um sistema é igual à diferença entre o calor e o trabalho trocados pelo sistema com o meio exterior."

Considerando-se para fins ilustrativos um sistema composto por um gás com apenas movimentos translacionais (isso é, monoatômico) e sem interação potencial entre partículas, a variação de energia interna pode ser determinada por

ΔU=32nR(Tf−Ti){displaystyle Delta U={frac {3}{2}}nR(T_{f}-T_{i})},^{[Ref. 11][Ref. 3]}

onde n é o número de mols do gás, R é a constante dos gases, Tf{displaystyle T_{f}} a temperatura final e Ti{displaystyle T_{i}} a temperatura inicial do gás.

Repare que para um gás ideal a variação em sua energia interna está associada apenas à variação em sua temperatura. Transformações isotérmicas envolvendo um gás ideal implicam portanto que o trabalho W realizado pelo sistema sobre a vizinhança iguala-se em módulo ao calor que entra no sistema oriundo da vizinhança.

Para a aplicação do primeiro princípio de termodinâmica devem-se respeitar as seguintes convenções^{[Ref. 11][Ref. 3]}:

• Q > 0: calor é recebido pelo sistema oriundo de sua vizinhança.


• Q < 0: calor cedido pelo sistema à vizinhança.


• W > 0: volume do sistema aumenta; o sistema realiza trabalho sobre a vizinhança (cujo volume diminui).


• W < 0: volume do sistema diminui; o sistema recebe energia na forma de trabalho oriunda de sua vizinhança (cujo volume aumenta).


• 
  ΔU{displaystyle Delta U} > 0: a energia interna do sistema aumenta.


• 
  ΔU{displaystyle Delta U} < 0: a energia interna do sistema diminui.

É muito comum associar-se de forma errônea o aumento da energia interna em um sistema a um aumento em sua temperatura. Embora esta relação mostre-se verdadeira para a maioria dos sistemas, ao rigor da análise esta associação não procede. Alguns exemplos bem simples, como a combustão de vapor de gasolina e oxigênio em um cilindro de automóvel - que por ser muito rápida, pode ser considerada um processo adiabático - ou uma simples mistura de sal e gelo, mostram que não há uma relação estrita entre energia interna e temperatura, mas sim entre energia térmica e temperatura.

A transformação que leva o sistema termodinâmico do estado A até o estado B é isobárica.

Na combustão do vapor de gasolina e oxigênio formam-se vapor de água e gás carbônico que, ao fim, estão em temperatura muito maior do que a temperatura dos reagentes. Contudo a energia interna do sistema não varia. O que ocorre é a transformação de parte da energia potencial - uma das parcelas que integram a energia interna - do sistema em energia térmica, a outra parcela que a integra. Como o aumento na energia térmica é inteiramente oriundo da diminuição da energia potencial (energia química) do sistema, a energia interna permanece a mesma, e não há variação na energia interna do sistema, mesmo observando-se um enorme aumento em sua temperatura.

Caso contrário é observado em um sistema composto por gelo e sal mantidos separados. Removendo-se a fronteira que os separa, a temperatura da mistura salina que se forma cai drasticamente, contudo a energia interna do sistema, assumido envolto por uma fronteira completamente restritiva (um sistema isolado), permanece constante. Parte da energia térmica é utilizada para romper-se as ligações iônicas associada à forma cristalina do sal - liquefazendo a mistura - e transformando-se por tal em energia potencial. O decréscimo na energia térmica é contudo compensado pelo acréscimo na energia potencial, de forma que a energia interna - conforme exigido pela fronteira restritiva - não varia, embora a temperatura caia substancialmente.

Podemos dizer que a energia interna do sistema é uma função de estado pois ela depende unicamente dos valores assumidos pelas variáveis de estado do sistema, e não da forma como tais variáveis assumiram tais valores. Em outras palavras, a energia interna de uma xícara de café quente com mesma composição química, mesma concentração, mesma massa, quando submetida à mesma pressão, volume e temperatura, será sempre a mesma, independente de como se fez o café, ou se este foi feito agora, ou requentado.

Repare que a energia interna é função apenas da temperatura somente para casos especiais, como o caso do gás ideal. Para casos genéricos não pode-se assumir tal conjectura como verdadeira. A energia interna pode depender da pressão, do volume, e de qualquer outra grandeza termodinâmica de forma explicita.

Quanto ao trabalho realizado pelo sistema sobre sua vizinhança, este pode ser facilmente determinado em transformações isobáricas - aquelas nas quais a pressão permanece constante - por:

W=p(V2−V1){displaystyle W=p(V_{2}-V_{1})}^{[Ref. 11][Ref. 3]}

onde V₂ e V₁ representam os volumes final e inicial do sistema, respectivamente. Repare a convenção a origem da convenção de sinais: quando o gás realiza trabalho sobre o meio - expandindo-se contra a pressão imposta pelo mesmo e gastando parte de sua energia interna para tal - o sinal do trabalho é positivo (volume aumenta), o qual, substituído na expressão matemática do primeiro princípio, implica um decréscimo da energia interna do sistema em virtude do sinal negativo presente nesta última expressão.

Em casos mais complexos, o trabalho pode ser determinado através de um diagrama de pressão x volume para a transformação sofrida. Este corresponde à área sob a região determinada pelos estados inicial, final, e pela curva associada (vide figuras abaixo).

Princípio segundo: uma passagem só de ida |

A termodinâmica permite determinar a direção na qual vários processos físicos e químicos irão ocorrer espontaneamente, e as condições para que possam ser revertidos (reversibilidade). Permite também determinar quais processos podem ocorrer, e quais não podem (irreversibilidade). Também permite determinar as inter-relações entre as diversas propriedades de uma substância, a exemplo calor específico, coeficiente de dilatação volumétrica, compressibilidade, e demais. Contudo ela não encerra em sua descrição macroscópica dados relativos aos modelos da microestrutura da substância, e não é capaz de fornecer detalhes dela partindo-se apenas das grandezas macroscópicas. Contudo, uma vez que a estrutura microscópica do sistema seja previamente conhecida, através do método da termodinâmica clássica e estatística, as propriedades e o comportamento termodinâmicos do sistema podem ser em princípio facilmente determinados.^{[Ref. 3]}

Em sistemas adiabáticos determinados processos ocorrem em sentido único, sendo impossível, sem violar-se a restrição adiabática imposta pela barreira, regressar-se ao estado original. Associado à irreversibilidade de tais processos tem-se a segunda lei da termodinâmica: em processos adiabáticos, a entropia do sistema permanece constante ou aumenta, contudo nunca diminui. Se um processo qualquer - geralmente processos bruscos, como a expansão livre - implicar em aumento da entropia do sistema, o estado inicial - de menor entropia - torna-se inacessível ao sistema sem violação da restrição imposta. Após uma expansão livre não se consegue mais retornar às mesmas condições de pressão, volume e temperatura iniciais sem a violação da fronteira adiabática do sistema.^{[Ref. 3]}

A 2ª Lei da termodinâmica estabelece portanto uma seta para o tempo: estabelece em essência a possibilidade de se definir com precisão uma ordem cronológica para uma série de eventos relacionados. Estabelece que energia cinética macroscopicamente mensurável pode sempre reduzir-se, mediante trabalho, a calor, e desta forma acabar fazendo parte das entranhas de um sistema termodinâmico - ou seja, da energia interna deste - contudo o processo inverso jamais ocorre com rendimento de 100%. Calor oriundo da energia interna de um sistema não pode ser totalmente convertido em trabalho, e por tal jamais é completamente convertido em energia cinética macroscopicamente mensurável. Decorre desta certamente considerações estimulantes tanto de ordem filosófica como de ordem científica ligadas às implicações da mesma, a exemplo considerações sobre a possível morte térmica do universo.^{[Ref. 11]}

Transformações termodinâmicas particulares |

Transformação isotérmica^{[Ref. 11][Ref. 12]}: transformação realizada de forma que a temperatura do sistema permaneça sempre constante.

Para gases ideais, implica que a quantidade de calor que o gás recebe seja exatamente igual ao trabalho por ele realizado.

Transformação isocórica ou Transformação isovolumétrica^{[Ref. 11][Ref. 12]}: como o volume do sistema se mantém constante, não há realização de trabalho.

O calor trocado com o meio externo corresponde à variação da energia interna do sistema.

A curva hiperbólica que liga os pontos A e B representa uma transformação isotérmica em um gás perfeito.

Transformação isobárica^{[Ref. 11][Ref. 12]}: Trata-se de uma transformação onde a pressão do sistema permanece sempre a mesma.

Parte do calor que o sistema troca com o meio externo está relacionado com o trabalho realizado e o restante com a variação da energia interna do sistema.

Transformação adiabática^{[Ref. 12]}: há uma fronteira restritiva quanto ao calor entre sistema e vizinhança. Não há calor, e a única forma de se fazer a energia interna variar é mediante a realização de trabalho.

Numa expansão adiabática, o sistema realiza trabalho sobre o meio às expensas da energia interna deste.

Durante a compressão adiabática, o meio realiza trabalho sobre o sistema e a energia interna aumenta.

Transformação cíclica^{[Ref. 11][Ref. 12]}

Denomina-se transformação cíclica ou ciclo de um sistema o conjunto de transformações sofridas pelo sistema de tal forma que seus estados final e inicial sejam iguais.

Como as variáveis de estado finais e iniciais são iguais, a energia interna do sistema não varia, bem como sua energia térmica - diretamente associada à temperatura. Há assim uma igualdade entre o calor e o trabalho trocados em cada ciclo.

Num diagrama p x V uma transformação cíclica é representada por uma curva fechada. A área interna do ciclo é numericamente igual ao trabalho total trocado com o meio exterior.

Quando o ciclo completo é percorrido no sentido horário, o sistema recebe calor e realiza trabalho (o trabalho W e o calor Q totais são ambos positivos); no sentido anti-horário o sistema cede calor e recebe trabalho (o trabalho W e o calor Q totais são ambos negativos),ou seja:

W_ciclo>0 e Q_ciclo >0 em ciclo horário, implicando em uma máquina térmica.

Q<0_ciclo ; W_ciclo<0 em ciclo anti-horário, implicando em um refrigerador térmico (como as geladeiras)

Em uma transformação cíclica existe equivalência entre o calor Q trocado pelo gás e o trabalho realizado. Repare contudo que estes valores não são sempre iguais ao longo do ciclo, o que equivale a dizer que a energia interna pode variar e geralmente varia ao longo do ciclo. Contudo o saldo final por ciclo implica uma variação da energia interna nula, e um trabalho total por ciclo igual ao calor envolvido por ciclo.

Leis da Termodinâmica |

A termodinâmica é baseada em leis estabelecidas experimentalmente:

• A Lei Zero da Termodinâmica^{[Ref. 3][Ref. 12]}determina que, quando dois sistemas em equilíbrio termodinâmico têm igualdade de temperatura com um terceiro sistema também em equilíbrio, eles têm igualdade de temperatura entre si. Esta lei é a base empírica para a medição de temperatura. Ela também estabelece o que vem a ser um sistema em equilíbrio termodinâmico: dado tempo suficiente, um sistema isolado atingirá um estado final - o estado de equilíbrio termodinâmico - onde nenhuma transformação macroscópica será doravante observada, caracterizando-se este por uma homogeneidade das grandezas termodinâmicas ao longo de todo o sistema (temperatura, pressão, volumes parciais ... constantes).


• A Primeira Lei da Termodinâmica^{[Ref. 3][Ref. 12]}fornece o aspecto quantitativo de processos de conversão de energia. É o princípio da conservação da energia e da conservação da massa, agora familiar, : "A energia do Universo, sistema mais vizinhança, é constante".


• A Segunda Lei da Termodinâmica^{[Ref. 3][Ref. 12]}determina de forma quantitativa a viabilidade de processos em sistemas físicos no que se refere à possibilidade de troca de energia e à ocorrência ou não destes processos na natureza. Afirma que há processos que ocorrem numa certa direção mas não podem ocorrer na direção oposta. Foi enunciada por Clausius da seguinte maneira: "A entropia do Universo, [sistema mais vizinhança], tende a um máximo": somente processos que levem a um aumento, ou quando muito à manutenção, da entropia total do sistema mais vizinhança são observados na natureza. Em sistemas isolados, transformações que impliquem uma diminuição em sua entropia jamais ocorrerão.


• A Terceira Lei da Termodinâmica^{[Ref. 3][Ref. 12]}estabelece um ponto de referência absoluto para a determinação da entropia, representado pelo estado derradeiro de ordem molecular máxima e mínima energia. Enunciada como "A entropia de uma substância cristalina pura na temperatura zero absoluto é zero".

Propriedades básicas |

Símbolos

Nome	Dimensão/ Valor	Unidade
T{displaystyle ~T}	Temperatura absoluta	K
p;P{displaystyle ~p;P}[35]	Pressão	Pa
V{displaystyle ~V}	Volume	m³
Wcp{displaystyle ~W_{cp}}	Média de energia de uma molécula	J
WKcp{displaystyle ~W_{Kcp}}	média de energia cinética uma molécula	J
m{displaystyle ~m}	Massa	kg
μ,M{displaystyle ~mu ,M}[36]	Massa molar	kg/mol
NA{displaystyle ~N_{A}}	Constante de Avogadro	6.0221415(10)×1023 mol -1
k{displaystyle ~k}	Constante de Boltzmann	1.3806505(24)×10−23 J / K
R{displaystyle ~R}	Constante do Gás	8.314472(15) J/(К·mol)	R=k⋅NA{displaystyle ~R=kcdot N_{A}}
i{displaystyle ~i}	Número de graus de liberdade da molécula	-
Nj,j=1,...n{displaystyle ~N_{j},,j=1,...n}	Quantidade de substância j{displaystyle j}-O componente n{displaystyle n}-mistura componental	mol
N{displaystyle ~N}	Vetor com coordenadas Nj,j=1,...n{displaystyle N_{j},,j=1,...n}	mol
μj,j=1,...n{displaystyle ~mu _{j},,j=1,...n}	Potencial Químico j{displaystyle j}-Componentes n{displaystyle n}- mistura de Componentes	J/mol
U{displaystyle ~U}	Energia interna	J
S{displaystyle ~S}	Entropia	J/К
H=U+PV{displaystyle ~H=U+PV}	Entalpia	J
F=U−TS{displaystyle ~F=U-TS}  A=U−TS{displaystyle ~A=U-TS}[37]	Condições isovolumétricas-isotérmicas do potencial de Helmholtz (energia livre)	J
G=H−TS{displaystyle ~G=H-TS}	potencial isobárico, isotérmico (energia livre de Gibbs, entalpia livre)	J
W;A{displaystyle ~W;A}	Trabalho realizado pelo gás	J
Q{displaystyle ~Q}	Calor transferido para o gás	J
CP{displaystyle ~C_{P}}	Capacidade térmica molar a pressão constante	J/(К·моl)
CV{displaystyle ~C_{V}}	Capacidade térmica molar a um volume constante	J/(К·mol)
c{displaystyle ~c}	Capacidade térmica específica	J/(К·kg)
γ{displaystyle ~gamma }	Sistema adiabático	-	γ=i+2i{displaystyle ~gamma ={frac {i+2}{i}}}

As fórmulas da termodinâmica do gás ideal |

 U=∑Wi=N⋅Wcp=mμNA⋅i2kT=i2mμRT=i2PV{displaystyle ~U=sum W_{i}=Ncdot W_{cp}={frac {m}{mu }}N_{A}cdot {frac {i}{2}}kT={frac {i}{2}}{frac {m}{mu }}RT={frac {i}{2}}PV}

Equação de estado do gás ideal ( equação de Mendeleyev-Klapeyrona )	PV=mμRT{displaystyle ~PV={frac {m}{mu }}RT}
Mudança da energia interna do gás	ΔU=Q−A{displaystyle ~Delta U=Q-A}
Trabalho do Gás	A=∫PdV{displaystyle ~A=int Pmathrm {d} V}
Média de energia de uma molécula de gás	Wcp=i2kT{displaystyle ~W_{cp}={frac {i}{2}}kT}
Média de Energia cinética de uma molécula de gás:	WKcp=32kT{displaystyle ~W_{Kcp}={frac {3}{2}}kT}
Energia interna do gás	U=i2PV{displaystyle ~U={frac {i}{2}}PV}  U=i2mμRT{displaystyle ~U={frac {i}{2}}{frac {m}{mu }}RT}

Capacidade térmica do Gás a volume constante:

 CV=i2R{displaystyle ~C_{V}={frac {i}{2}}R}

A quantidade de calor recebida por um corpo, é expressa através da sua massa, e a capacidade térmica conhecida através da fórmula:

 Q=mcΔT=mμCΔT.{displaystyle ~Q=mcDelta T={frac {m}{mu }}CDelta T.}

A quantidade de calor recebida é igualmente a mudança de energia interna:

 Q=ΔU=i2mμRΔT.{displaystyle ~Q=Delta U={frac {i}{2}}{frac {m}{mu }}RDelta T.}

Igualando as peças certas de ambas as equações, receberemos:

 mμCVΔT=i2mμRΔT;{displaystyle ~{frac {m}{mu }}C_{V}Delta T={frac {i}{2}}{frac {m}{mu }}RDelta T;}

 CV=i2R.{displaystyle ~C_{V}={frac {i}{2}}R.}

Capacidade térmica do gás a pressão constante

 CP=i+22R{displaystyle ~C_{P}={frac {i+2}{2}}R}

A quantidade de calor recebida por um corpo, é expressa através da sua massa, e a capacidade térmica conhecida através da fórmula:

 Q=mcΔT=mμCΔT.{displaystyle ~Q=mcDelta T={frac {m}{mu }}CDelta T.}

Como na quantidade do processo isobárico do calor recebido pelo gás é ,igualmente, a mudança de energia interna + o trabalho realizado pelo gás, vamos escrever:

 Q=ΔU+ΔA=i2mμRΔT+PΔV=i2mμRΔT+mμRΔT=i+22⋅mμRΔT.{displaystyle ~Q=Delta U+Delta A={frac {i}{2}}{frac {m}{mu }}RDelta T+PDelta V={frac {i}{2}}{frac {m}{mu }}RDelta T+{frac {m}{mu }}RDelta T={frac {i+2}{2}}cdot {frac {m}{mu }}RDelta T.}

Igualando as peças certas de ambas as equações, receberemos:

 mμCPΔT=i+22⋅mμRΔT;{displaystyle ~{frac {m}{mu }}C_{P}Delta T={frac {i+2}{2}}cdot {frac {m}{mu }}RDelta T;}

 CP=i+22R.{displaystyle ~C_{P}={frac {i+2}{2}}R.}

Expressão dos potenciais termodinâmicos |

Todos os potenciais termodinâmicos, possuem conjuntos de variáveis e são utilizados para a análise dos processos sob condições correspondentes. Assim para processos isotérmicos (T,V=const{displaystyle T,V=const}) é conveniente usar F(N,T,V){displaystyle F(N,T,V)}, para a Transformação isobárica(T,P=const{displaystyle T,P=const}) — G(N,T,P){displaystyle G(N,T,P)},e para os sistemas isolados: (U,V=const{displaystyle U,V=const}) — S(N,U,V){displaystyle S(N,U,V)}.

Potencial Termodinâmico S(N,U,V){displaystyle S(N,U,V)} (entropia) |

• 
  N,U,V{displaystyle N,,U,,V} — variáveis independentes (fator que não é influenciado pelo valor de outros fatores)


• 
  T=(∂S∂U)−1{displaystyle T=left({frac {partial S}{partial U}}right)^{-1}};


• 
  P=∂S∂V(∂S∂U)−1{displaystyle P={frac {partial S}{partial V}}left({frac {partial S}{partial U}}right)^{-1}};


• 
  μj=−∂S∂Nj(∂S∂U)−1{displaystyle mu _{j}=-{frac {partial S}{partial N_{j}}}left({frac {partial S}{partial U}}right)^{-1}};


• 
  H=U+V∂S∂V(∂S∂U)−1{displaystyle H=U+V{frac {partial S}{partial V}}left({frac {partial S}{partial U}}right)^{-1}};


• 
  F=U−S(∂S∂U)−1{displaystyle F=U-Sleft({frac {partial S}{partial U}}right)^{-1}};


• 
  G=U+(S∂S∂V−S)(∂S∂U)−1{displaystyle G=U+left(S{frac {partial S}{partial V}}-Sright)left({frac {partial S}{partial U}}right)^{-1}}.

Potencial Termodinâmico F(N,T,V){displaystyle F(N,T,V)} (Energia livre de Helmholtz) |

• 
  N,T,V{displaystyle N,,T,,V} — variáveis independentes (fator que não é influenciado pelo valor de outros fatores)


• 
  S=−∂F∂T{displaystyle S=-{frac {partial F}{partial T}}};


• 
  P=−∂F∂V{displaystyle P=-{frac {partial F}{partial V}}};


• 
  μj=∂F∂Nj{displaystyle mu _{j}={frac {partial F}{partial N_{j}}}};


• 
  U=F−T∂F∂T{displaystyle U=F-T{frac {partial F}{partial T}}};


• 
  H=F−T∂F∂T−V∂F∂V{displaystyle H=F-T{frac {partial F}{partial T}}-V{frac {partial F}{partial V}}};


• 
  G=F−V∂F∂V{displaystyle G=F-V{frac {partial F}{partial V}}}.

Potencial Termodinâmico U(N,S,V){displaystyle U(N,S,V)} (Energia interna) |

• 
  N,S,V{displaystyle N,,S,,V} — variáveis independentes (fator que não é influenciado pelo valor de outros fatores)


• 
  T=∂U∂S{displaystyle T={frac {partial U}{partial S}}};


• 
  P=−∂U∂V{displaystyle P=-{frac {partial U}{partial V}}};


• 
  μj=∂U∂Nj{displaystyle mu _{j}={frac {partial U}{partial N_{j}}}};


• 
  H=U−V∂U∂V{displaystyle H=U-V{frac {partial U}{partial V}}};


• 
  F=U−S∂U∂S{displaystyle F=U-S{frac {partial U}{partial S}}};


• 
  G=U−V∂U∂V−S∂U∂S{displaystyle G=U-V{frac {partial U}{partial V}}-S{frac {partial U}{partial S}}}.

A equação fundamental de Gibbs |

Uma expressão para a diferença de energia interna é chamada de equação fundamental de Gibbs ou simples equação de Gibbs :

dU=TdS−PdV+∑jμjdNj.{displaystyle dU=TdS-PdV+sum _{j}mu _{j}dN_{j},.}

A importância dessa equação consiste em que ela representa a base sobre a qual todos os modernos aparelhos matemáticos de fenomenologia termodinâmica, tanto os conceitos de equilíbrio e não-equilíbrio, são baseados.
A equação de Gibbs pode ser representada para uso de outros potenciais termodinâmicos equivalentes nas seguintes formulações:

dG=−SdT+VdP+∑jμjdNj;{displaystyle dG=-SdT+VdP+sum _{j}mu _{j}dN_{j},;}

dF=−SdT−PdV+∑jμjdNj.{displaystyle dF=-SdT-PdV+sum _{j}mu _{j}dN_{j},.}

Ver também |

• Sistema termodinâmico


• Calorimetria


• Ciclo termodinâmico


• Escalas termométricas


• Termologia

Notas

Referências

O Wikilivros tem um livro chamado Curso de termodinâmica

v • e Campos de estudo da Física
Mecânica clássica	Cinemática Estática Dinâmica Mecânica dos corpos rígidos Mecânica dos fluidos Mecânica de Lagrange Mecânica hamiltoniana
Ondulatória	Acústica Óptica
Termofísica	Termodinâmica Calorimetria Teoria cinética dos gases Mecânica estatística
Eletromagnetismo	Eletricidade Eletromagnetismo Eletrostática Magnetostática Magnetismo Óptica
Relatividade	Relatividade restrita Relatividade geral
Mecânica quântica	Mecânica ondulatória Teoria quântica de campos
Física aplicada	Físico-química Astrofísica Geofísica Biofísica Física médica Física matemática Meteorologia física
Matéria condensada	Física mesoscópica

• Portal da física