Gravidade
A gravitação mantém os planetas em órbita ao redor do Sol. (Sem escala.)
A gravidade é uma das quatro forças fundamentais da natureza, em conjunto com o eletromagnetismo, a força fraca e a força forte.[1] Na física moderna, a descrição mais precisa da gravidade é dada pela teoria geral da relatividade de Einstein, segundo a qual o fenómeno é uma consequência da curvatura espaço-tempo que regula o movimento de objetos inertes. A clássica lei da gravitação universal de Newton postula que a força da gravidade é diretamente proporcional às massas dos corpos em interação e inversamente proporcional ao quadrado da distância entre eles. Esta descrição oferece uma aproximação precisa para a maioria das situações físicas, entre as quais os cálculos de trajetória espacial.[2]
Do ponto de vista prático, a atração gravitacional da Terra confere peso aos objetos e faz com que caiam ao chão quando são soltos (como a atração é mútua, a Terra também se move em direção aos objetos, mas apenas por uma ínfima fração).[2]
Do ponto de vista cosmológico, a gravidade faz com que a matéria dispersa se aglutine, e que essa matéria aglutinada se mantenha intacta, permitindo dessa forma a existência de planetas, estrelas, galáxias e a maior parte dos objetos macroscópicos no universo. A gravidade é ainda responsável por manter a Terra e os demais planetas e satélites em suas respectivas órbitas, pela formação das marés pela convecção natural, por aquecer o interior de estrelas e planetas em formação e por vários outros fenómenos na Terra e no universo.
Índice
1 Lei de Newton de gravitação universal
1.1 Forma vetorial
1.2 Aceleração da gravidade
1.3 Comparação com a força eletromagnética
2 História
3 A teoria geral da relatividade de Einstein
3.1 Constante cosmológica
4 Mecânica quântica
5 Comparação da força da gravidade no Sistema Solar
6 Outras teorias gravitacionais
7 Ver também
8 Referências
8.1 Bibliográficas
8.2 Leitura adicional
9 Ligações externas
Lei de Newton de gravitação universal

Sir Isaac Newton, físico britânico que viveu de 1642 a 1727
Gravitação é a força de atração que existe entre todas as partículas com massa no universo. A gravitação é responsável por prender objectos à superfície de planetas e, de acordo com as leis do movimento de Newton, é responsável por manter objectos em órbita em torno uns dos outros. A gravidade faz muito mais do que simplesmente segurar-nos às nossas cadeiras.
Foi Isaac Newton quem a reconheceu. Newton escreveu numa das suas memórias que na altura em que estava a tentar compreender o que mantinha a Lua no céu viu uma maçã cair no seu pomar, e compreendeu que a Lua não estava suspensa no céu mas sim que caía continuamente, como se fosse uma bola de canhão que fosse disparada com tanta velocidade que nunca atinge o chão por este também "cair" devido à curvatura da Terra.
Segundo a terceira lei de Newton, quaisquer dois objectos exercem uma atracção gravitacional um sobre o outro de igual valor e sentido oposto. Pouco se sabia sobre gravitação até o século XVII, pois acreditava-se que leis diferentes governavam os céus e a Terra. A força que mantinha a Lua pendurada no céu nada tinha a ver com a força que nos mantém presos à Terra. Isaac Newton foi o primeiro a pensar na hipótese das duas forças possuírem as mesmas naturezas; até então, havia apenas a teoria magnetista de Johannes Kepler, que dizia que era o magnetismo que fazia os planetas orbitarem o Sol.
Newton explica, "Todos os objectos no Universo atraem todos os outros objectos com uma força direccionada ao longo da linha que passa pelos centros dos dois objectos, e que é proporcional ao produto das suas massas e inversamente proporcional ao quadrado da separação entre os dois objectos."
Newton acabou por publicar a sua, ainda hoje famosa, lei da gravitação universal, no seu Principia Mathematica, como:
- F=Gm1m2r2{displaystyle F={frac {Gm_{1}m_{2}}{r^{2}}}}
onde:
- F = força gravitacional entre dois objectos
- m1 = massa do primeiro objecto
- m2 = massa do segundo objecto
- r = distância entre os centros de massa dos objectos
- G = constante universal da gravitação
A força de atração entre dois objetos é chamada de peso.
Rigorosamente falando, esta lei aplica-se apenas a objectos semelhantes a pontos. Se os objectos possuírem extensão espacial, a verdadeira força terá de ser encontrada pela integração das forças entre os vários pontos. Por outro lado, pode provar-se que para um objecto com uma distribuição de massa esfericamente simétrica, a integral resulta na mesma atracção gravitacional que teria se fosse uma massa pontual.
Foi este obstáculo que levou Newton a adiar por vários anos a publicação da sua teoria, já que ele não conseguia mostrar que a gravitação exercida pela Terra sobre um corpo à sua superfície era a mesma como se toda a massa da Terra estivesse concentrada em seu centro.[3]
Forma vetorial
A forma anteriormente descrita é uma versão simplificada. Ela é expressa mais propriamente pela forma que segue, a qual é vetorialmente completa (Todas as grandezas em negrito representam grandezas vetoriais).
- F12=Gm1m2(r2−r1)|r2−r1|3{displaystyle mathbf {F_{1,2}} ={Gm_{1}m_{2}(mathbf {r_{2}} -mathbf {r_{1}} ) over left|mathbf {r_{2}} -mathbf {r_{1}} right|^{3}}}
e que:
F12{displaystyle mathbf {F_{1,2}} }é a força exercida em m1{displaystyle m_{1}}por m2{displaystyle m_{2}}
.
m1{displaystyle m_{1}}e m2{displaystyle m_{2}}
são as massas
r1{displaystyle mathbf {r_{1}} }er2{displaystyle mathbf {r_{2}} }são os vectores posição das duas massas respectivas
G{displaystyle G}é a constante gravitacional
Para a força na massa dois, simplesmente tome o oposto do vetor F12{displaystyle mathbf {F_{1,2}} }
A principal diferença entre as duas formulações é que a segunda forma usa a diferença na posição para construir um vetor que aponta de uma massa para a outra, e de seguida divide o vetor pelo seu módulo para evitar que mude a magnitude da força.
Aceleração da gravidade
O exemplo mais conhecido de movimento uniforme acelerado é o de um corpo em queda livre. Um corpo em queda livre em direção à superfície da Terra apenas sob ação da gravidade, acelerará a uma taxa de 9,80665 m/s² (32,174 pés/s) por cada segundo que o corpo esta caindo. Este valor é conhecido como aceleração padrão da gravidade ou constante gravitacional universal. Esta lei Newtoniana conclui que “duas partículas se atraem com forças cuja intensidade é diretamente proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância que as separa”.[4][5]
A aceleração da gravidade é uma aceleração física de um objeto causado pela força da gravidade. Desprezando atrito tais como a resistência ao ar, todas as massas pequenas se aceleram num campo gravitacional com a mesma taxa em relação ao centro de massa.[6] Esta igualdade é verdade independentemente das massas ou composições dos corpos.
Comparação com a força eletromagnética
A atração gravitacional dos prótons é aproximadamente um fator 10 36 mais fraco que a repulsão electromagnética. Este fator é independente de distância, porque ambas as forças são inversamente proporcionais ao quadrado da distância. Isso significa que, numa balança atômica, a gravidade mútua é desprezável. Porém, a força principal entre os objetos comuns e a Terra e entre corpos celestiais é a gravidade, quando pelo menos um deles é eletricamente neutro, ou quase. Contudo se em ambos os corpos houvesse um excesso ou déficit de único elétron para cada 10 18 prótons isto já seria suficiente para cancelar a gravidade (ou no caso de um excesso num e um déficit no outro: duplicar a atração).
A relativa fraqueza da gravidade pode ser demonstrada com um pequeno ímã, que vai atraindo para cima pedaços de ferro pousados no chão. O minúsculo ímã consegue anular a força gravitacional da Terra inteira.
A gravidade é pequena, a menos que a massa de um dos dois corpos seja grande, mas a pequena força gravitacional exercida por corpos de tamanho ordinário pode ser demonstrada com razoável facilidade por experiências como a da barra de torção de Cavendish.
História
Ninguém tem certeza se o conto sobre Newton e a maçã é verídico, mas o raciocínio, com certeza, tem seu valor. Ninguém antes dele ousou contrariar Aristóteles e dizer que a mesma força que atrai uma maçã para o chão mantém a Lua, a Terra, e todos os planetas em suas órbitas.
Newton não foi o único a fazer contribuições significativas para o entendimento da gravidade. Antes dele, Galileu Galilei corrigiu uma noção comum, partida do mesmo Aristóteles, de que objetos de massas diferentes caem com velocidades diferentes. Para Aristóteles, simplesmente fazia sentido que objetos de massas diferentes demorassem tempos diferentes a cair da mesma altura e isso era o bastante para ele. Galileu, no entanto, tentou de fato lançar objetos de massas diferentes ao mesmo tempo e da mesma altura. Desprezando as diferenças devido ao arraste do ar, Galileu observou que todas as massas aceleravam igualmente. Podemos deduzir isso usando a Segunda Lei de Newton, F=ma{displaystyle F=ma}



- m1a1=F1=−Gm1MTr2{displaystyle m_{1}a_{1}=F_{1}=-{Gm_{1}M_{T} over r^{2}}}
- m2a2=F2=−Gm2MTr2{displaystyle m_{2}a_{2}=F_{2}=-{Gm_{2}M_{T} over r^{2}}}
Dividindo a primeira equação por m1{displaystyle m_{1}}

- a1=−GMTr2{displaystyle a_{1}=-{GM_{T} over r^{2}}}
- a2=−GMTr2{displaystyle a_{2}=-{GM_{T} over r^{2}}}
ou seja, a1=a2{displaystyle a_{1}=a_{2}}
A teoria geral da relatividade de Einstein
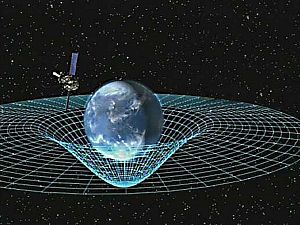
Analogia bidimensional da distorção no espaço-tempo gerada pela massa de um objecto. A matéria altera a geometria do espaço-tempo, esta (curva) geométrica que é interpretado como gravidade.
A formulação da gravidade por Newton é bastante precisa para a maioria dos propósitos práticos. Existem, no entanto, alguns problemas:[7]
- Assume que alterações na força gravitacional são transmitidas instantaneamente quando a posição dos corpos gravitantes muda. Porém, isto contradiz o fato que existe uma velocidade limite a que podem ser transmitidos os sinais (velocidade da luz no vácuo).
- O pressuposto de espaço e tempo absolutos contradiz a teoria de relatividade especial de Einstein.
- Prediz que a luz é desviada pela gravidade apenas metade do que é efectivamente observado.
- Não explica buracos negros,
- De acordo com a gravidade newtoniana (com transmissão instantânea de força gravitacional), se o Universo é euclidiano, estático, de densidade uniforme em média positiva e infinito, a força gravitacional total num ponto é uma série divergente. Por outras palavras, a gravidade newtoniana é incompatível com um Universo com estas propriedades.
Uma das questões da teoria de Einstein, a existência das ondas gravitacionais, foi comprovada em Fevereiro de 2016 pelo projeto LIGO.
Para o primeiro destes problemas, Einstein desenvolveu uma nova teoria da gravidade chamada relatividade geral, publicada em 1915. Nesta teoria ele estabelece o chamado princípio da equivalência, onde não há como um observador distinguir localmente se está num campo gravitacional ou em movimento acelerado. Esta teoria também prediz que a presença de matéria "distorce" o ambiente de espaço-tempo local, fazendo com que linhas aparentemente "rectas" no espaço e no tempo tenham características que são normalmente associadas a linha "curvas".
Embora a relatividade geral seja, enquanto teoria, mais precisa que a lei de Newton, requer também um formalismo matemático significativamente mais complexo. Ele introduziu o conceito de espaço-tempo curvo, o que não permite a simplicidade da métrica euclidiana. Em vez de descrever o efeito de gravitação como uma "força real" derivada da atração entre as massas, Einstein a coloca na mesma categoria das "forças inerciais" pelo princípio da equivalência.
A teoria da relatividade de Einstein prediz que a velocidade da gravidade (definida como a velocidade a que mudanças na localização de uma massa são propagadas a outras massas) deve ser consistente com a velocidade da luz. Em 2002, a experiência de Fomalont-Kopeikin produziu medições da velocidade da gravidade que corresponderam a esta predição. No entanto, esta experiência ainda não sofreu um processo amplo de revisão pelos pares, e está a encontrar cepticismo por parte dos que afirmam que Fomalont-Kopeikin não fez mais do que medir a velocidade da luz de uma forma intrincada.
Constante cosmológica
Ao escrever a equação da gravitação segundo a Relatividade Geral, Einstein introduziu um termo chamado de constante cosmológica, para que a solução das equações fossem um universo estático. Ao tomar conhecimento da expansão do Universo, Einstein removeu este termo, dizendo que este foi o seu maior erro.
Esta constante tem sido objeto de estudo, para explicar o período conhecido como inflação cósmica. O efeito da constante cosmológica seria análogo a uma "gravidade repulsiva", e, no tempo presente, causaria uma aceleração da expansão do Universo.
Mecânica quântica
A força da gravidade é, das quatro forças da natureza, a única que obstinadamente se recusa a ser quantizada (as outras três - o eletromagnetismo, a força forte e a força fraca podem ser quantizadas). Quantização significa que a força pode ser medida em partes discretas que não podem ser diminuídas em tamanho, não importando o que aconteça; alternativamente, essa interação gravitacional é transmitida por partículas chamadas gravitons. Cientistas têm estudado sobre o graviton por anos, mas têm tido apenas frustrações nas suas buscas para encontrar uma consistente teoria quântica sobre isso. Muitos acreditam que a Teoria de cordas alcançará o grande objetivo de unir Relatividade Geral e Mecânica Quântica, mas essa promessa ainda não se realizou.
Comparação da força da gravidade no Sistema Solar
A aceleração devido à gravidade à superfície da Terra é 9,80665 m/s² (o valor real varia ligeiramente ao longo da superfície da Terra; ver g para mais detalhes). Esta medida é conhecida como gn, ge, g0, ou simplesmente g. A lista que se segue apresenta a força da gravidade (em múltiplos de g) na superfície dos planetas do Sistema Solar[Nota 1].
| Nome | Comparação com a Terra | Aceleração da gravidade |
|---|---|---|
| Sol | 27,95 | 274,13 m/s² |
| Mercúrio | 0.376 | 3,7 m/s² |
| Vénus | 0.903 | 8,87 m/s² |
| Terra | 1 | 9,807 m/s² |
| Lua | 0,17 | 1,622 m/s² |
| Marte | 0.38 | 3,711 m/s² |
Júpiter[Nota 2] | 2.52 | 24,79 m/s² |
Europa (Satélite de Júpiter) | 1,315 m/s² | |
Saturno[Nota 2] | 1.06 | 10,44 m/s² |
Titã (Satélite de Saturno) | 1,352 m/s² | |
Urano[Nota 2] | 0.89 | 8,69 m/s² |
Netuno[Nota 2] | 1.14 | 11,15 m/s² |
|
Nos corpos esféricos, a gravidade superficial em m/s² é 2.8 × 10−10 vezes o raio em m vezes a densidade média em kg/m³.
Outras teorias gravitacionais
- Teoria aristotélica da gravitação
Teoria gravitacional de Le Sage (1784) proposta por Georges-Louis Le Sage
Teoria de gravitação de Nordström (1912, 1913)
Teoria de gravitação de Whitehead (1922)
Teoria de Brans–Dicke(1961)
Gravidade induzida (1967), uma proposta de Andrei Sakharov segundo a qual a teoria da relatividade geral teria origem na teoria quântica de campos
- Na dinâmica newtoniana modificada (MOND) (1981), Mordehai Milgrom propõe uma modificação na segunda lei de Newton para pequenas acelerações.
- Teorias gravitacionais de cosmologia de autocriação, de G.A. Barber, no qual a teoria de Brans-Dicke é modificada para permitir a criação em massa.
Teoria da gravitação assimétrica (NGT) (1994) de John Moffat
Gravidade tensor-vetor-escalar (TeVeS) (2004), uma modificação relativística de MOND por Jacob Bekenstein
Ver também
- Constante gravitacional universal
- Efeito de Eötvös
- Força inercial de Coriolis
- Gravidade artificial
- Imponderabilidade
- Massa
- Peso
- Radiação gravitacional
Referências
↑ Does Gravity Travel at the Speed of Light?, UCR Mathematics. 1998. Retrieved 3 July 2008
↑ ab «Gravidade». Porto Editora. Infopédia
↑ Pannekoek, Anton. A History of Astronomy. Dover Publications, 1989. ISBN 0486659941
↑ Dossat, Roy J. (2004). Princípios de refrigeração. [S.l.]: Hemus. p. 12. ISBN 8528901599
↑ Toffoli, Leopoldo. «Lei da Gravitação Universal». InfoEscola. Consultado em 5 de fevereiro de 2014
↑ James Holton, Gerald; Brush, Stephen G. (2001). Physics, the human adventure: from Copernicus to Einstein and beyond (3ª ed.). Rutgers University Press. p. 113. ISBN 978-0-8135-2908-0.
↑ Rosa, Guilherme (25 de abril de 2013). «Astrônomos confirmam (mais uma vez) teoria de Einstein». Abril. Veja. Consultado em 5 de fevereiro de 2014
Bibliográficas
Halliday, David; Robert Resnick; Kenneth S. Krane (2001). Physics v. 1 (em inglês). Nova Iorque: John Wiley & Sons. ISBN 0-471-32057-9 A referência emprega parâmetros obsoletos|coautor=(ajuda)
Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (em inglês) 6ª ed. [S.l.]: Brooks/Cole. ISBN 0-534-40842-7 A referência emprega parâmetros obsoletos|coautor=(ajuda)
Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (em inglês) 5ª ed. [S.l.]: W. H. Freeman. ISBN 0-7167-0809-4
Leitura adicional
Thorne, Kip S.; Misner, Charles W.; Wheeler, John Archibald (1973). Gravitation (em inglês). [S.l.]: W.H. Freeman. ISBN 0-7167-0344-0 A referência emprega parâmetros obsoletos|coautor=(ajuda)
Ligações externas
O que é gravidade (em português) - Revista Nova Escola
Hazewinkel, Michiel, ed. (2001), «Gravitation», Encyclopedia of Mathematics, ISBN 978-1-55608-010-4 (em inglês), Springer
Hazewinkel, Michiel, ed. (2001), «Gravitation, theory of», Encyclopedia of Mathematics, ISBN 978-1-55608-010-4 (em inglês), Springer







