Vrftsjtryk

Das Trigonale Kristallsystem gehört zu den sieben Kristallsystemen in der Kristallographie. Es umfasst alle Punktgruppen mit einer dreizähligen Dreh- oder Drehinversionsachse. Das trigonale Kristallsystem ist mit dem hexagonalen Kristallsystem eng verwandt und bildet zusammen mit ihm die hexagonale Kristallfamilie.

Die trigonalen Punktgruppen |

Das trigonale Kristallsystem umfasst die Punktgruppen 3,3¯,32,3m,3¯m{displaystyle 3,,{bar {3}},,32,,3m,,{bar {3}}m}. Dies sind alle die Punktgruppen der hexagonalen Kristallfamilie, in denen es eine Raumgruppe mit rhomboedrischer Zentrierung gibt – die Raumgruppen des hexagonalen Kristallsystems können alle mit dem hexagonal primitiven Achsensystem beschrieben werden.
Das trigonale Kristallsystem umfasst somit alle Untergruppen der Punktgruppe 3¯m{displaystyle {bar {3}}m}, die eine 3-zählige Achse haben. Im Gegensatz zu den hexagonalen Punktgruppen haben diese Punktgruppen alle eine kubische Obergruppe. Folgende Tabelle liefert einen Überblick über die Raumgruppen des trigonalen Kristallsystems.

Punktgruppe	Primitive Raumgruppen	Zentrierte Raumgruppen
C3{displaystyle C_{3}},  3{displaystyle 3}	P3,P31,P32{displaystyle P3,,P3_{1},,P3_{2}}	R3{displaystyle R3}
C3i(≡S6){displaystyle C_{3i}(equiv S_{6})}, 3¯{displaystyle {bar {3}}}	P3¯{displaystyle P{bar {3}}}	R3¯{displaystyle R{bar {3}}}
D3{displaystyle D_{3}},  32{displaystyle 32}	P312,P321,P3112,P3121P3212,P3221{displaystyle P312,,P321,,P3_{1}12,,P3_{1}21,P3_{2}12,,P3_{2}21}	R32{displaystyle R32}
C3v{displaystyle C_{3v}},  3m{displaystyle 3m}	P3m1,P31m,P3c1,P31c{displaystyle P3m1,,P31m,,P3c1,,P31c}	R3m,R3c{displaystyle R3m,,R3c}
D3d{displaystyle D_{3d}}, 3¯m{displaystyle {bar {3}}m}	P3¯1m,P3¯1c,P3¯1c,P3¯c1{displaystyle P{bar {3}}1m,,P{bar {3}}1c,,P{bar {3}}1c,,P{bar {3}}c1}	R3¯m,R3¯c{displaystyle R{bar {3}}m,,R{bar {3}}c}

Die Achsensysteme des trigonalen Kristallsystems |

Zur Beschreibung trigonaler Raumgruppen finden zwei verschiedene Gitter-Systeme Verwendung: das hexagonale und das rhomboedrische. Diese sind im Artikel hexagonales Kristallsystem ausführlich beschrieben. Die Begriffe trigonal und rhomboedrisch sind im modernen Sprachgebrauch klar abgegrenzt:

• Trigonal ist die Bezeichnung für eine Menge von Symmetriegruppen.


• Rhomboedrisch ist die Bezeichnung eines Gitter-Systems.

Punktgruppen im trigonalen Kristallsystem und ihre physikalischen Eigenschaften |

Zur Beschreibung der trigonalen Kristallklassen in Hermann-Mauguin-Symbolik werden die Symmetrieoperationen bezüglich vorgegebener Richtungen im Gitter-System angegeben.

Im hexagonalen Achsensystem: 1. Symbol in Richtung der c-Achse (<001>). 2. Symbol in Richtung einer a-Achse (<100>). 3. Symbol in einer Richtung senkrecht zu einer a- und der c-Achse (<120>). Für die 3. Richtung wird auch oftmals die im Allgemeinen nicht äquivalente Richtung <210> angegeben. Auch wenn dies speziell für die Angabe der Lage der Symmetrieelemente keine Rolle spielt, so entspricht diese Angabe nicht den Konventionen.

Im rhomboedrischen Achsensystem: 1. Symbol in Richtung der Raumdiagonalen (<111>). 2. Symbol in Richtung einer Flächendiagonalen (<110>).

Charakteristisch für alle Raumgruppen des trigonalen Kristallsystems ist die 3 (oder 3) an 1. Stelle des Raumgruppensymbols.

Weitere trigonal kristallisierende chemische Stoffe siehe Kategorie:Trigonales Kristallsystem

Kristallformen des trigonalen Kristallsystems |

• 
  

  

  
  

  
  

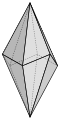
  Ditrigonales Skalenoeder
  

  
  

  
  


• 
  

  

  
  

  
  

  Trigonales Trapezoeder
  

  
  

  
  


• 
  

  

  
  

  
  

  Quarzkristall
  

  
  

  
  

Literatur |

• W. Borchardt-Ott: Kristallographie. 6. Auflage. Springer, Berlin 2002, ISBN 3-540-43964-1.


• W. Massa: Kristallstrukturbestimmung. 3. Auflage. Teubner, Stuttgart 2002, ISBN 3-519-23527-7.


• M. Okrusch, S. Matthes: Mineralogie. 7. Auflage. Springer, Berlin 2005, ISBN 3-540-23812-3.


• Hahn, Theo (Hrsg.): International Tables for Crystallography Vol. A D. Reidel publishing Company, Dordrecht 1983, ISBN 90-277-1445-2
  

Weblinks |

• 
  Kurzskript Algebra I – Kristallographie. Uni Dortmund, S. 11 (PDF, 412 kB).