Intuition behind Matrix Multiplication
$begingroup$
If I multiply two numbers, say $3$ and $5$, I know it means add $3$ to itself $5$ times or add $5$ to itself $3$ times.
But If I multiply two matrices, what does it mean ? I mean I can't think it in terms of repetitive addition.
What is the intuitive way of thinking about multiplication of matrices?
matrices intuition faq
$endgroup$
|
show 8 more comments
$begingroup$
If I multiply two numbers, say $3$ and $5$, I know it means add $3$ to itself $5$ times or add $5$ to itself $3$ times.
But If I multiply two matrices, what does it mean ? I mean I can't think it in terms of repetitive addition.
What is the intuitive way of thinking about multiplication of matrices?
matrices intuition faq
$endgroup$
67
$begingroup$
Do you think of $3.9289482948290348290 times 9.2398492482903482390$ as repetitive addition?
$endgroup$
– lhf
Apr 8 '11 at 12:43
13
$begingroup$
It depends on what you mean by 'meaning'.
$endgroup$
– Mitch
Apr 8 '11 at 12:58
17
$begingroup$
I believe a more interesting question is why matrix multiplication is defined the way it is.
$endgroup$
– M.B.
Apr 8 '11 at 13:01
5
$begingroup$
I can't help but read your question's title in Double-Rainbow-man's voice...
$endgroup$
– Adrian Petrescu
Apr 8 '11 at 16:04
4
$begingroup$
You probably want to read this answer of Arturo Magidin's: Matrix Multiplication: Interpreting and Understanding the Multiplication Process
$endgroup$
– Uticensis
Apr 8 '11 at 16:42
|
show 8 more comments
$begingroup$
If I multiply two numbers, say $3$ and $5$, I know it means add $3$ to itself $5$ times or add $5$ to itself $3$ times.
But If I multiply two matrices, what does it mean ? I mean I can't think it in terms of repetitive addition.
What is the intuitive way of thinking about multiplication of matrices?
matrices intuition faq
$endgroup$
If I multiply two numbers, say $3$ and $5$, I know it means add $3$ to itself $5$ times or add $5$ to itself $3$ times.
But If I multiply two matrices, what does it mean ? I mean I can't think it in terms of repetitive addition.
What is the intuitive way of thinking about multiplication of matrices?
matrices intuition faq
matrices intuition faq
edited Aug 10 '13 at 15:28
Jeel Shah
5,291115599
5,291115599
asked Apr 8 '11 at 12:41
Happy MittalHappy Mittal
1,27941727
1,27941727
67
$begingroup$
Do you think of $3.9289482948290348290 times 9.2398492482903482390$ as repetitive addition?
$endgroup$
– lhf
Apr 8 '11 at 12:43
13
$begingroup$
It depends on what you mean by 'meaning'.
$endgroup$
– Mitch
Apr 8 '11 at 12:58
17
$begingroup$
I believe a more interesting question is why matrix multiplication is defined the way it is.
$endgroup$
– M.B.
Apr 8 '11 at 13:01
5
$begingroup$
I can't help but read your question's title in Double-Rainbow-man's voice...
$endgroup$
– Adrian Petrescu
Apr 8 '11 at 16:04
4
$begingroup$
You probably want to read this answer of Arturo Magidin's: Matrix Multiplication: Interpreting and Understanding the Multiplication Process
$endgroup$
– Uticensis
Apr 8 '11 at 16:42
|
show 8 more comments
67
$begingroup$
Do you think of $3.9289482948290348290 times 9.2398492482903482390$ as repetitive addition?
$endgroup$
– lhf
Apr 8 '11 at 12:43
13
$begingroup$
It depends on what you mean by 'meaning'.
$endgroup$
– Mitch
Apr 8 '11 at 12:58
17
$begingroup$
I believe a more interesting question is why matrix multiplication is defined the way it is.
$endgroup$
– M.B.
Apr 8 '11 at 13:01
5
$begingroup$
I can't help but read your question's title in Double-Rainbow-man's voice...
$endgroup$
– Adrian Petrescu
Apr 8 '11 at 16:04
4
$begingroup$
You probably want to read this answer of Arturo Magidin's: Matrix Multiplication: Interpreting and Understanding the Multiplication Process
$endgroup$
– Uticensis
Apr 8 '11 at 16:42
67
67
$begingroup$
Do you think of $3.9289482948290348290 times 9.2398492482903482390$ as repetitive addition?
$endgroup$
– lhf
Apr 8 '11 at 12:43
$begingroup$
Do you think of $3.9289482948290348290 times 9.2398492482903482390$ as repetitive addition?
$endgroup$
– lhf
Apr 8 '11 at 12:43
13
13
$begingroup$
It depends on what you mean by 'meaning'.
$endgroup$
– Mitch
Apr 8 '11 at 12:58
$begingroup$
It depends on what you mean by 'meaning'.
$endgroup$
– Mitch
Apr 8 '11 at 12:58
17
17
$begingroup$
I believe a more interesting question is why matrix multiplication is defined the way it is.
$endgroup$
– M.B.
Apr 8 '11 at 13:01
$begingroup$
I believe a more interesting question is why matrix multiplication is defined the way it is.
$endgroup$
– M.B.
Apr 8 '11 at 13:01
5
5
$begingroup$
I can't help but read your question's title in Double-Rainbow-man's voice...
$endgroup$
– Adrian Petrescu
Apr 8 '11 at 16:04
$begingroup$
I can't help but read your question's title in Double-Rainbow-man's voice...
$endgroup$
– Adrian Petrescu
Apr 8 '11 at 16:04
4
4
$begingroup$
You probably want to read this answer of Arturo Magidin's: Matrix Multiplication: Interpreting and Understanding the Multiplication Process
$endgroup$
– Uticensis
Apr 8 '11 at 16:42
$begingroup$
You probably want to read this answer of Arturo Magidin's: Matrix Multiplication: Interpreting and Understanding the Multiplication Process
$endgroup$
– Uticensis
Apr 8 '11 at 16:42
|
show 8 more comments
14 Answers
14
active
oldest
votes
$begingroup$
Matrix ¨multiplication¨ is the composition of two linear functions. The composition of two linear functions is a linear function.
If a linear function is represented by A and another by B then AB is their composition. BA is the their reverse composition.
Thats one way of thinking of it. It explains why matrix multiplication is the way it is instead of piecewise multiplication.
$endgroup$
32
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
2
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
2
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
add a comment |
$begingroup$
Asking why matrix multiplication isn't just componentwise multiplication is an excellent question: in fact, componentwise multiplication is in some sense the most "natural" generalization of real multiplication to matrices: it satisfies all of the axioms you would expect (associativity, commutativity, existence of identity and inverses (for matrices with no 0 entries), distributivity over addition).
The usual matrix multiplication in fact "gives up" commutativity; we all know that in general AB != BA while for real numbers ab = ba. What do we gain? Invariance with respect to change of basis. If P is an invertible matrix,
$$P^{-1}AP + P^{-1}BP = P^{-1}(A+B)P$$
$$(P^{-1}AP) (P^{-1}BP) = P^{-1}(AB)P$$
In other words, it doesn't matter what basis you use to represent the matrices A and B, no matter what choice you make their sum and product is the same.
It is easy to see by trying an example that the second property does not hold for multiplication defined component-wise. This is because the inverse of a change of basis $P^{-1}$ no longer corresponds to the multiplicative inverse of $P$.
$endgroup$
26
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
1
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
add a comment |
$begingroup$
The short answer is that a matrix corresponds to a linear transformation. To multiply two matrices is the same thing as composing the corresponding linear transformations (or linear maps).
The following is covered in a text on linear algebra (such as Hoffman-Kunze):
This makes most sense in the context of vector spaces over a field. You can talk about vector spaces and (linear) maps between them without ever mentioning a basis. When you pick a basis, you can write the elements of your vector space as a sum of basis elements with coefficients in your base field (that is, you get explicit coordinates for your vectors in terms of for instance real numbers). If you want to compute something, you typically pick bases for your vector spaces. Then you can represent your linear map as a matrix with respect to the given bases, with entries in your base field (see e.g. the above mentioned book for details as to how). We define matrix multiplication such that matrix multiplication corresponds to composition of the linear maps.
Added (Details on the presentation of a linear map by a matrix). Let $V$ and $W$ be two vector spaces with ordered bases $e_1,dots,e_n$ and $f_1,dots,f_m$ respectively, and $L:Vto W$ a linear map.
First note that since the $e_j$ generate $V$ and $L$ is linear, $L$ is completely determined by the images of the $e_j$ in $W$, that is, $L(e_j)$. Explicitly, note that by the definition of a basis any $vin V$ has a unique expression of the form $a_1e_1+cdots+a_ne_n$, and $L$ applied to this pans out as $a_1L(e_1)+cdots+a_nL(e_n)$.
Now, since $L(e_j)$ is in $W$ it has a unique expression of the form $b_1f_1+dots+b_mf_m$, and it is clear that the value of $e_j$ under $L$ is uniquely determined by $b_1,dots,b_m$, the coefficients of $L(e_j)$ with respect to the given ordered basis for $W$. In order to keep track of which $L(e_j)$ the $b_i$ are meant to represent, we write (abusing notation for a moment) $m_{ij}=b_i$, yielding the matrix $(m_{ij})$ of $L$ with respect to the given ordered bases.
This might be enough to play around with why matrix multiplication is defined the way it is. Try for instance a single vector space $V$ with basis $e_1,dots,e_n$, and compute the corresponding matrix of the square $L^2=Lcirc L$ of a single linear transformation $L:Vto V$, or say, compute the matrix corresponding to the identity transformation $vmapsto v$.
$endgroup$
add a comment |
$begingroup$
By Flanigan & Kazdan:
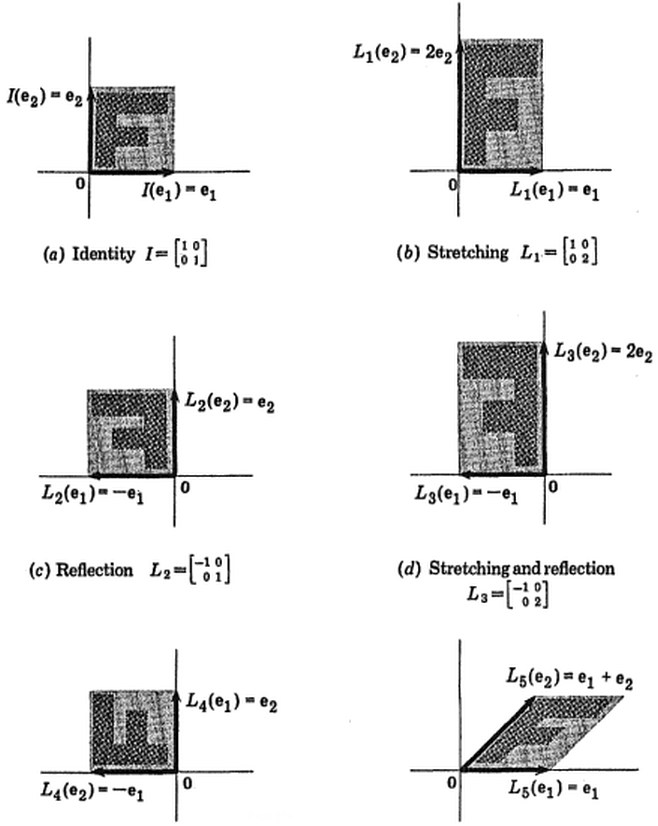

Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)
This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 Box ^2_3 {} xrightarrow{mathbf{V} updownarrow} {} ^4_1 Box ^3_2 {} xrightarrow{Theta_{90} curvearrowright} {} ^1_2 Box ^4_3 $$ versus $$^1_4 Box ^2_3 {} xrightarrow{Theta_{90} curvearrowright} {} ^4_3 Box ^1_2 {} xrightarrow{mathbf{V} updownarrow} {} ^3_4 Box ^2_1 $$
The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).


You could also watch the matrices work on Mona step by step too, to help your intuition.
Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 overset{f}{longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg.  ) which is an "even"
) which is an "even"  stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other
stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.
$endgroup$
1
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
add a comment |
$begingroup$
Apart from the interpretation as the composition of linear functions (which is, in my opinion, the most natural one), another viewpoint is on some occasions useful.
You can view them as something akin to a generalization of elementary row/column operations. If you compute $AB$, then the coefficients in $j$-th row of $A$ tell you, which linear combination of rows of B you should compute and put into the $j$-th row of the new matrix.
Similarly, you can view $AB$ as making linear combinations of columns of $A$, with the coefficients prescribed by the matrix $B$.
With this viewpoint in mind you can easily see that, if you denote by $vec{a}_1,dots,vec a_k$ the rows of the matrix $A$, then the equality
$$begin{pmatrix}vec a_1\vdots\vec a_kend{pmatrix}B=
begin{pmatrix}vec a_1B\vdots\vec a_kBend{pmatrix}$$
holds. (Of course, you can obtain this equality directly from definition or by many other methods. My intention was to illustrate a situation, when familiarity this viewpoint could be useful.)
$endgroup$
1
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
add a comment |
$begingroup$
First, Understand Vector multiplication by a scalar.
Then, think on a Matrix, multiplicated by a vector. The Matrix is a "vector of vectors".
Finally, Matrix X Matrix extends the former concept.
$endgroup$
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
1
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
1
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
add a comment |
$begingroup$
Suppose
begin{align}
p & = 2x + 3y \
q & = 3x - 7y \
r & = -8x+9y
end{align}
Represent this way from transforming $begin{bmatrix} x \ y end{bmatrix}$ to $begin{bmatrix} p \ q \ r end{bmatrix}$ by the matrix
$$
left[begin{array}{rr} 2 & 3 \ 3 & -7 \ -8 & 9 end{array}right].
$$
Now let's transform $begin{bmatrix} p \ q \ r end{bmatrix}$ to $begin{bmatrix} a \ b end{bmatrix}$:
begin{align}
a & = 22p-38q+17r \
b & = 13p+10q+9r
end{align}
represent that by the matrix
$$
left[begin{array}{rr} 22 & -38 & 17 \ 13 & 10 & 9 end{array}right].
$$
So how do we transform $begin{bmatrix} x \ y end{bmatrix}$ directly to $begin{bmatrix} a \ b end{bmatrix}$?
Do a bit of algebra and you get
begin{align}
a & = bullet, x + bullet, y \
b & = bullet, x + bullet, y
end{align}
and you should be able to figure out what numbers the four $bullet$s are. That matrix of four $bullet$s is what you get when you multiply those earlier matrices. That's why matrix multiplication is defined the way it is.
$endgroup$
2
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
|
show 1 more comment
$begingroup$
To get away from how these two kinds of multiplications are implemented (repeated addition for numbers vs. row/column dot product for matrices) and how they behave symbolically/algebraically (associativity, distribute over 'addition', have annihilators, etc), I'd like to answer in the manner 'what are they good for?'
Multiplication of numbers gives area of a rectangle with sides given by the multiplicands (or number of total points if thinking discretely).
Multiplication of matrices (since it involves quite a few more actual numbers than just simple multiplication) is understandably quite a bit more complex. Though the composition of linear functions (as mentioned elsewhere) is the essence of it, that's not the most intuitive description of it (to someone without the abstract algebraic experience). A more visual intuition is that one matrix, multiplying with another, results in the transformation of a set of points (the columns of the right-hand matrix) into new set of points (the columns of the resulting matrix). That is, take a set of $n$ points in $n$ dimensions, put them as columns in an $ntimes n$ matrix; if you multiply this from the left by another $n times n$ matrix, you'll transform that 'cloud' of points to a new cloud.
This transformation isn't some random thing; it might rotate the cloud, it might expand the cloud, it won't 'translate' the cloud, it might collapse the cloud into a line (a lower number of dimensions might be needed). But it's transforming the whole cloud all at once smoothly (near points get translated to near points).
So that is one way of getting the 'meaning' of matrix multiplication.
I have a hard time getting a good metaphor (any metaphor) between matrix multiplication and simple numerical multiplication so I won't force it - hopefully someone else might be able to come up with a better visualization that shows how they're more alike beyond the similarity of some algebraic properties.
$endgroup$
add a comment |
$begingroup$
You shouldn't try to think in terms of scalars and try to fit matrices into this way of thinking.
It's exactly like with real and complex numbers. It's difficult to have an intuition about complex operations if you try to think in terms of real operations.
scalars are a special case of matrices, as real numbers are a special case of complex numbers.
So you need to look at it from the other, more abstract side. If you think about real operations in terms of complex operations, they make complete sense (they are a simple case of the complex operations).
And the same is true for Matrices and scalars. Think in terms of matrix operations and you will see that the scalar operations are a simple (special) case of the corresponding matrix operations.
$endgroup$
add a comment |
$begingroup$
One way to try to "understand" it would be to think of two factors in the product of two numbers as two different entities: one is multiplying and the other is being multiplied. For example, in $5cdot4$, $5$ is the one that is multiplying $4$, and $4$ is being multiplied by $5$. You can think in terms of repetitive addition that you are adding $4$ to itself $5$ times: You are doing something to $4$ to get another number, that something is characterized by the number $5$. We forbid the interpretation that you are adding $5$ to itself $4$ times here, because $5cdot$ is an action that is related to the number $5$, it is not a number. Now, what happens if you multiply $4$ by $5$, and then multiply the result by $3$? In other words,
$3cdot(5cdot4)=?$
or more generally,
$3cdot(5cdot x)=?$
when we want to vary the number being multiplied. Think of for example, we need to multiply a lot of different numbers $x$ by $5$ first and then by $3$, and we want to somehow simplify this process, or to find a way to compute this operation fast.
Without going into the details, we all know the above is equal to
$3cdot(5cdot x)=(3times 5)cdot x$,
where
$3times 5$ is just the ordinary product of two numbers, but I used different notation to emphasize that this time we are multiplying "multipliers" together, meaning that the result of this operation is an entity that multiplies other numbers, in contrast to the result of $5cdot4$, which is an entity that gets multiplied. Note that in some sense, in $3times5$ the numbers $5$ and $3$ participates on an equal ground, while in $5cdot4$ the numbers have differing roles. For the operation $times$ no interpretation is available in terms of repetitive addition, because we have two actions, not an action and a number. In linear algebra, the entities that gets multiplied are vectors, the "multiplier" objects are matrices, the operation $cdot$ generalizes to the matrix-vector product, and the operation $times$ extends to the product between matrices.
$endgroup$
add a comment |
$begingroup$
Let's say you're multiplying matrix $A$ by matrix $B$ and producing $C$:
$A times B = C$
At a high level, $A$ represents a set of linear functions or transformations to apply, $B$ is a set of values for the input variables to run through the linear functions/transformations, and $C$ is the result of applying the linear functions/transformations to the input values.
For more details, see below:
(1) $A$ consists of rows, each of which corresponds to a linear function/transformation
For instance, let's say the first row in $A$ is $[a_1 , a_2 , a_3]$ where $a_1$, $a_2$ and $a_3$ are constants. Such row corresponds to the linear function/transformation:
$$f(x, y, z) = a_1x + a_2y + a_3z$$
(2) $B$ consists of columns, each of which corresponds to values for the input variables.
For instance, let's say the first column in $B$ consists of the values $[b_1 , b_2 , b_3]$ (transpose). Such column correspond to setting the input variable values as follows:
$$x=b_1 \ y=b_2 \ z=b_3$$
(3) $C$ consists of entries whereby an entry at row $i$ and column $j$ corresponds to applying the linear function/transformation represented in $A$'s $i$th row to the input variable values provided by $B$'s $j$th column.
Thus, the entry in the first row and first column of $C$ in the example discussed thus far, would equate to:
begin{align}
f(x=b_1, y=b_2, z=b_3) &= a_1x + a_2y + a_3z \
&= a_1b_1 + a_2b_2 + a_3b_3
end{align}
$endgroup$
add a comment |
$begingroup$
Instead of trying to explain it, I will link you to an interactive graphic. As you play around with it, watch how the matrix in the top left corner changes as you move X' and Y'. The intuition for how matrix multiplication works comes after the intuition for where it's used. https://www.geogebra.org/m/VjhNaB8V
$endgroup$
add a comment |
$begingroup$
Let's explain where matrices and matrix multiplication come from. But first a bit of notation: $e_i$ denotes the column vector in $mathbb R^n$ which has a 1 in the $i$th position and zeros elsewhere:
$$
e_1 = begin{bmatrix} 1 \ 0 \ 0 \ vdots \ 0 end{bmatrix},
e_2 = begin{bmatrix} 0 \ 1 \ 0 \ vdots \ 0 end{bmatrix},
ldots,
e_n = begin{bmatrix} 0 \ 0 \ 0 \ vdots \ 1 end{bmatrix}
.
$$
Suppose that $T:mathbb R^n to mathbb R^m$ is a linear transformation.
The matrix
$$
A = begin{bmatrix} T(e_1) & cdots & T(e_n) end{bmatrix}
$$
is called the matrix description of $T$.
If we are given $A$, then we can easily compute $T(x)$ for any vector $x in mathbb R^n$, as follows: If
$$
x = begin{bmatrix} x_1 \ vdots \ x_n end{bmatrix}
$$
then
$$
tag{1}T(x) = T(x_1 e_1 + cdots + x_n e_n) = x_1 underbrace{T(e_1)}_{text{known}} + cdots + x_n underbrace{T(e_n)}_{text{known}}.
$$
In other words, $T(x)$ is a linear combination of the columns of $A$. To save writing, we will denote this particular linear combination as $Ax$:
$$
Ax = x_1 cdot left(text{first column of $A$}right) + x_2 cdot left(text{second column of $A$}right) + cdots + x_n cdot left(text{final column of $A$} right).
$$
With this notation, equation (1) can be written as
$$
T(x) = Ax.
$$
Now suppose that $T:mathbb R^n to mathbb R^m$ and $S:mathbb R^m to mathbb R^p$ are linear transformations, and that $T$ and $S$ are represented by the matrices $A$ and $B$ respectively.
Let $a_i$ be the $i$th column of $A$.
Question: What is the matrix description of $S circ T$?
Answer: If $C$ is the matrix description of $S circ T$, then the $i$th column of $C$ is
begin{align}
c_i &= (S circ T)(e_i) \
&= S(T(e_i)) \
&= S(a_i) \
&= B a_i.
end{align}
For this reason, we define the "product" of $B$ and $A$ to be the matrix whose $i$th column is $B a_i$. With this notation, the matrix description of $S circ T$ is
$$
C = BA.
$$
If you write everything out in terms of components, you will observe that this definition agrees with the usual definition of matrix multiplication.
That is how matrices and matrix multiplication can be discovered.
$endgroup$
add a comment |
$begingroup$
This is the detailed and easiest explanation : https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
$endgroup$
add a comment |
Your Answer
StackExchange.ifUsing("editor", function () {
return StackExchange.using("mathjaxEditing", function () {
StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
});
});
}, "mathjax-editing");
StackExchange.ready(function() {
var channelOptions = {
tags: "".split(" "),
id: "69"
};
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function() {
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled) {
StackExchange.using("snippets", function() {
createEditor();
});
}
else {
createEditor();
}
});
function createEditor() {
StackExchange.prepareEditor({
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader: {
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
},
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
});
}
});
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f31725%2fintuition-behind-matrix-multiplication%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
14 Answers
14
active
oldest
votes
14 Answers
14
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Matrix ¨multiplication¨ is the composition of two linear functions. The composition of two linear functions is a linear function.
If a linear function is represented by A and another by B then AB is their composition. BA is the their reverse composition.
Thats one way of thinking of it. It explains why matrix multiplication is the way it is instead of piecewise multiplication.
$endgroup$
32
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
2
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
2
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
add a comment |
$begingroup$
Matrix ¨multiplication¨ is the composition of two linear functions. The composition of two linear functions is a linear function.
If a linear function is represented by A and another by B then AB is their composition. BA is the their reverse composition.
Thats one way of thinking of it. It explains why matrix multiplication is the way it is instead of piecewise multiplication.
$endgroup$
32
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
2
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
2
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
add a comment |
$begingroup$
Matrix ¨multiplication¨ is the composition of two linear functions. The composition of two linear functions is a linear function.
If a linear function is represented by A and another by B then AB is their composition. BA is the their reverse composition.
Thats one way of thinking of it. It explains why matrix multiplication is the way it is instead of piecewise multiplication.
$endgroup$
Matrix ¨multiplication¨ is the composition of two linear functions. The composition of two linear functions is a linear function.
If a linear function is represented by A and another by B then AB is their composition. BA is the their reverse composition.
Thats one way of thinking of it. It explains why matrix multiplication is the way it is instead of piecewise multiplication.
answered Apr 8 '11 at 13:00
SearkeSearke
1,322198
1,322198
32
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
2
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
2
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
add a comment |
32
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
2
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
2
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
32
32
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
$begingroup$
Actually, I think it's the only (sensible) way of thinking of it. Textbooks which only give the definition in terms of coordinates, without at least mentioning the connection with composition of linear maps, (such as my first textbook on linear algebra!) do the student a disservice.
$endgroup$
– wildildildlife
Apr 8 '11 at 16:26
2
2
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Learners, couple this knowledge with mathinsight.org/matrices_linear_transformations . It may save you a good amount of time. :)
$endgroup$
– n611x007
Jan 30 '13 at 16:36
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
$begingroup$
Indeed, there is a sense in which all associative binary operators with an identity element are represented as composition of functions - that is the underlying nature of associativity. (If there isn't an identity, you get a representation as composition, but it might not be faithful.)
$endgroup$
– Thomas Andrews
Aug 10 '13 at 15:30
2
2
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
$begingroup$
can you give an example of what you mean?
$endgroup$
– Goldname
Mar 11 '16 at 21:18
add a comment |
$begingroup$
Asking why matrix multiplication isn't just componentwise multiplication is an excellent question: in fact, componentwise multiplication is in some sense the most "natural" generalization of real multiplication to matrices: it satisfies all of the axioms you would expect (associativity, commutativity, existence of identity and inverses (for matrices with no 0 entries), distributivity over addition).
The usual matrix multiplication in fact "gives up" commutativity; we all know that in general AB != BA while for real numbers ab = ba. What do we gain? Invariance with respect to change of basis. If P is an invertible matrix,
$$P^{-1}AP + P^{-1}BP = P^{-1}(A+B)P$$
$$(P^{-1}AP) (P^{-1}BP) = P^{-1}(AB)P$$
In other words, it doesn't matter what basis you use to represent the matrices A and B, no matter what choice you make their sum and product is the same.
It is easy to see by trying an example that the second property does not hold for multiplication defined component-wise. This is because the inverse of a change of basis $P^{-1}$ no longer corresponds to the multiplicative inverse of $P$.
$endgroup$
26
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
1
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
add a comment |
$begingroup$
Asking why matrix multiplication isn't just componentwise multiplication is an excellent question: in fact, componentwise multiplication is in some sense the most "natural" generalization of real multiplication to matrices: it satisfies all of the axioms you would expect (associativity, commutativity, existence of identity and inverses (for matrices with no 0 entries), distributivity over addition).
The usual matrix multiplication in fact "gives up" commutativity; we all know that in general AB != BA while for real numbers ab = ba. What do we gain? Invariance with respect to change of basis. If P is an invertible matrix,
$$P^{-1}AP + P^{-1}BP = P^{-1}(A+B)P$$
$$(P^{-1}AP) (P^{-1}BP) = P^{-1}(AB)P$$
In other words, it doesn't matter what basis you use to represent the matrices A and B, no matter what choice you make their sum and product is the same.
It is easy to see by trying an example that the second property does not hold for multiplication defined component-wise. This is because the inverse of a change of basis $P^{-1}$ no longer corresponds to the multiplicative inverse of $P$.
$endgroup$
26
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
1
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
add a comment |
$begingroup$
Asking why matrix multiplication isn't just componentwise multiplication is an excellent question: in fact, componentwise multiplication is in some sense the most "natural" generalization of real multiplication to matrices: it satisfies all of the axioms you would expect (associativity, commutativity, existence of identity and inverses (for matrices with no 0 entries), distributivity over addition).
The usual matrix multiplication in fact "gives up" commutativity; we all know that in general AB != BA while for real numbers ab = ba. What do we gain? Invariance with respect to change of basis. If P is an invertible matrix,
$$P^{-1}AP + P^{-1}BP = P^{-1}(A+B)P$$
$$(P^{-1}AP) (P^{-1}BP) = P^{-1}(AB)P$$
In other words, it doesn't matter what basis you use to represent the matrices A and B, no matter what choice you make their sum and product is the same.
It is easy to see by trying an example that the second property does not hold for multiplication defined component-wise. This is because the inverse of a change of basis $P^{-1}$ no longer corresponds to the multiplicative inverse of $P$.
$endgroup$
Asking why matrix multiplication isn't just componentwise multiplication is an excellent question: in fact, componentwise multiplication is in some sense the most "natural" generalization of real multiplication to matrices: it satisfies all of the axioms you would expect (associativity, commutativity, existence of identity and inverses (for matrices with no 0 entries), distributivity over addition).
The usual matrix multiplication in fact "gives up" commutativity; we all know that in general AB != BA while for real numbers ab = ba. What do we gain? Invariance with respect to change of basis. If P is an invertible matrix,
$$P^{-1}AP + P^{-1}BP = P^{-1}(A+B)P$$
$$(P^{-1}AP) (P^{-1}BP) = P^{-1}(AB)P$$
In other words, it doesn't matter what basis you use to represent the matrices A and B, no matter what choice you make their sum and product is the same.
It is easy to see by trying an example that the second property does not hold for multiplication defined component-wise. This is because the inverse of a change of basis $P^{-1}$ no longer corresponds to the multiplicative inverse of $P$.
answered Apr 8 '11 at 15:41
user7530user7530
35.1k861114
35.1k861114
26
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
1
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
add a comment |
26
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
1
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
26
26
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
$begingroup$
+1, but I can't help but point out that if componentwise multiplication is the most "natural" generalization, it is also the most boring generalization, in that under componentwise operations, a matrix is just a flat collection of $mn$ real numbers instead of being a new and useful structure with interesting properties.
$endgroup$
– Rahul
Apr 8 '11 at 17:09
1
1
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
$begingroup$
I don’t get it. For element-wise multiplication, we would define $P^{-1}$ as essentially element-wise reciprocals, so $PP^{-1}$ would be the identity, and the second property you mention would still hold. It is the essence of $P^{-1}$ to be the inverse of $P$. How else would you define $P^{-1}$?
$endgroup$
– Yatharth Agarwal
Nov 3 '18 at 20:27
add a comment |
$begingroup$
The short answer is that a matrix corresponds to a linear transformation. To multiply two matrices is the same thing as composing the corresponding linear transformations (or linear maps).
The following is covered in a text on linear algebra (such as Hoffman-Kunze):
This makes most sense in the context of vector spaces over a field. You can talk about vector spaces and (linear) maps between them without ever mentioning a basis. When you pick a basis, you can write the elements of your vector space as a sum of basis elements with coefficients in your base field (that is, you get explicit coordinates for your vectors in terms of for instance real numbers). If you want to compute something, you typically pick bases for your vector spaces. Then you can represent your linear map as a matrix with respect to the given bases, with entries in your base field (see e.g. the above mentioned book for details as to how). We define matrix multiplication such that matrix multiplication corresponds to composition of the linear maps.
Added (Details on the presentation of a linear map by a matrix). Let $V$ and $W$ be two vector spaces with ordered bases $e_1,dots,e_n$ and $f_1,dots,f_m$ respectively, and $L:Vto W$ a linear map.
First note that since the $e_j$ generate $V$ and $L$ is linear, $L$ is completely determined by the images of the $e_j$ in $W$, that is, $L(e_j)$. Explicitly, note that by the definition of a basis any $vin V$ has a unique expression of the form $a_1e_1+cdots+a_ne_n$, and $L$ applied to this pans out as $a_1L(e_1)+cdots+a_nL(e_n)$.
Now, since $L(e_j)$ is in $W$ it has a unique expression of the form $b_1f_1+dots+b_mf_m$, and it is clear that the value of $e_j$ under $L$ is uniquely determined by $b_1,dots,b_m$, the coefficients of $L(e_j)$ with respect to the given ordered basis for $W$. In order to keep track of which $L(e_j)$ the $b_i$ are meant to represent, we write (abusing notation for a moment) $m_{ij}=b_i$, yielding the matrix $(m_{ij})$ of $L$ with respect to the given ordered bases.
This might be enough to play around with why matrix multiplication is defined the way it is. Try for instance a single vector space $V$ with basis $e_1,dots,e_n$, and compute the corresponding matrix of the square $L^2=Lcirc L$ of a single linear transformation $L:Vto V$, or say, compute the matrix corresponding to the identity transformation $vmapsto v$.
$endgroup$
add a comment |
$begingroup$
The short answer is that a matrix corresponds to a linear transformation. To multiply two matrices is the same thing as composing the corresponding linear transformations (or linear maps).
The following is covered in a text on linear algebra (such as Hoffman-Kunze):
This makes most sense in the context of vector spaces over a field. You can talk about vector spaces and (linear) maps between them without ever mentioning a basis. When you pick a basis, you can write the elements of your vector space as a sum of basis elements with coefficients in your base field (that is, you get explicit coordinates for your vectors in terms of for instance real numbers). If you want to compute something, you typically pick bases for your vector spaces. Then you can represent your linear map as a matrix with respect to the given bases, with entries in your base field (see e.g. the above mentioned book for details as to how). We define matrix multiplication such that matrix multiplication corresponds to composition of the linear maps.
Added (Details on the presentation of a linear map by a matrix). Let $V$ and $W$ be two vector spaces with ordered bases $e_1,dots,e_n$ and $f_1,dots,f_m$ respectively, and $L:Vto W$ a linear map.
First note that since the $e_j$ generate $V$ and $L$ is linear, $L$ is completely determined by the images of the $e_j$ in $W$, that is, $L(e_j)$. Explicitly, note that by the definition of a basis any $vin V$ has a unique expression of the form $a_1e_1+cdots+a_ne_n$, and $L$ applied to this pans out as $a_1L(e_1)+cdots+a_nL(e_n)$.
Now, since $L(e_j)$ is in $W$ it has a unique expression of the form $b_1f_1+dots+b_mf_m$, and it is clear that the value of $e_j$ under $L$ is uniquely determined by $b_1,dots,b_m$, the coefficients of $L(e_j)$ with respect to the given ordered basis for $W$. In order to keep track of which $L(e_j)$ the $b_i$ are meant to represent, we write (abusing notation for a moment) $m_{ij}=b_i$, yielding the matrix $(m_{ij})$ of $L$ with respect to the given ordered bases.
This might be enough to play around with why matrix multiplication is defined the way it is. Try for instance a single vector space $V$ with basis $e_1,dots,e_n$, and compute the corresponding matrix of the square $L^2=Lcirc L$ of a single linear transformation $L:Vto V$, or say, compute the matrix corresponding to the identity transformation $vmapsto v$.
$endgroup$
add a comment |
$begingroup$
The short answer is that a matrix corresponds to a linear transformation. To multiply two matrices is the same thing as composing the corresponding linear transformations (or linear maps).
The following is covered in a text on linear algebra (such as Hoffman-Kunze):
This makes most sense in the context of vector spaces over a field. You can talk about vector spaces and (linear) maps between them without ever mentioning a basis. When you pick a basis, you can write the elements of your vector space as a sum of basis elements with coefficients in your base field (that is, you get explicit coordinates for your vectors in terms of for instance real numbers). If you want to compute something, you typically pick bases for your vector spaces. Then you can represent your linear map as a matrix with respect to the given bases, with entries in your base field (see e.g. the above mentioned book for details as to how). We define matrix multiplication such that matrix multiplication corresponds to composition of the linear maps.
Added (Details on the presentation of a linear map by a matrix). Let $V$ and $W$ be two vector spaces with ordered bases $e_1,dots,e_n$ and $f_1,dots,f_m$ respectively, and $L:Vto W$ a linear map.
First note that since the $e_j$ generate $V$ and $L$ is linear, $L$ is completely determined by the images of the $e_j$ in $W$, that is, $L(e_j)$. Explicitly, note that by the definition of a basis any $vin V$ has a unique expression of the form $a_1e_1+cdots+a_ne_n$, and $L$ applied to this pans out as $a_1L(e_1)+cdots+a_nL(e_n)$.
Now, since $L(e_j)$ is in $W$ it has a unique expression of the form $b_1f_1+dots+b_mf_m$, and it is clear that the value of $e_j$ under $L$ is uniquely determined by $b_1,dots,b_m$, the coefficients of $L(e_j)$ with respect to the given ordered basis for $W$. In order to keep track of which $L(e_j)$ the $b_i$ are meant to represent, we write (abusing notation for a moment) $m_{ij}=b_i$, yielding the matrix $(m_{ij})$ of $L$ with respect to the given ordered bases.
This might be enough to play around with why matrix multiplication is defined the way it is. Try for instance a single vector space $V$ with basis $e_1,dots,e_n$, and compute the corresponding matrix of the square $L^2=Lcirc L$ of a single linear transformation $L:Vto V$, or say, compute the matrix corresponding to the identity transformation $vmapsto v$.
$endgroup$
The short answer is that a matrix corresponds to a linear transformation. To multiply two matrices is the same thing as composing the corresponding linear transformations (or linear maps).
The following is covered in a text on linear algebra (such as Hoffman-Kunze):
This makes most sense in the context of vector spaces over a field. You can talk about vector spaces and (linear) maps between them without ever mentioning a basis. When you pick a basis, you can write the elements of your vector space as a sum of basis elements with coefficients in your base field (that is, you get explicit coordinates for your vectors in terms of for instance real numbers). If you want to compute something, you typically pick bases for your vector spaces. Then you can represent your linear map as a matrix with respect to the given bases, with entries in your base field (see e.g. the above mentioned book for details as to how). We define matrix multiplication such that matrix multiplication corresponds to composition of the linear maps.
Added (Details on the presentation of a linear map by a matrix). Let $V$ and $W$ be two vector spaces with ordered bases $e_1,dots,e_n$ and $f_1,dots,f_m$ respectively, and $L:Vto W$ a linear map.
First note that since the $e_j$ generate $V$ and $L$ is linear, $L$ is completely determined by the images of the $e_j$ in $W$, that is, $L(e_j)$. Explicitly, note that by the definition of a basis any $vin V$ has a unique expression of the form $a_1e_1+cdots+a_ne_n$, and $L$ applied to this pans out as $a_1L(e_1)+cdots+a_nL(e_n)$.
Now, since $L(e_j)$ is in $W$ it has a unique expression of the form $b_1f_1+dots+b_mf_m$, and it is clear that the value of $e_j$ under $L$ is uniquely determined by $b_1,dots,b_m$, the coefficients of $L(e_j)$ with respect to the given ordered basis for $W$. In order to keep track of which $L(e_j)$ the $b_i$ are meant to represent, we write (abusing notation for a moment) $m_{ij}=b_i$, yielding the matrix $(m_{ij})$ of $L$ with respect to the given ordered bases.
This might be enough to play around with why matrix multiplication is defined the way it is. Try for instance a single vector space $V$ with basis $e_1,dots,e_n$, and compute the corresponding matrix of the square $L^2=Lcirc L$ of a single linear transformation $L:Vto V$, or say, compute the matrix corresponding to the identity transformation $vmapsto v$.
edited Jul 4 '15 at 8:29
answered Apr 8 '11 at 13:04
Eivind DahlEivind Dahl
1,147614
1,147614
add a comment |
add a comment |
$begingroup$
By Flanigan & Kazdan:


Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)

This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 Box ^2_3 {} xrightarrow{mathbf{V} updownarrow} {} ^4_1 Box ^3_2 {} xrightarrow{Theta_{90} curvearrowright} {} ^1_2 Box ^4_3 $$ versus $$^1_4 Box ^2_3 {} xrightarrow{Theta_{90} curvearrowright} {} ^4_3 Box ^1_2 {} xrightarrow{mathbf{V} updownarrow} {} ^3_4 Box ^2_1 $$
The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).


You could also watch the matrices work on Mona step by step too, to help your intuition.
Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 overset{f}{longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg.  ) which is an "even"
) which is an "even"  stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other
stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.

$endgroup$
1
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
add a comment |
$begingroup$
By Flanigan & Kazdan:


Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)

This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 Box ^2_3 {} xrightarrow{mathbf{V} updownarrow} {} ^4_1 Box ^3_2 {} xrightarrow{Theta_{90} curvearrowright} {} ^1_2 Box ^4_3 $$ versus $$^1_4 Box ^2_3 {} xrightarrow{Theta_{90} curvearrowright} {} ^4_3 Box ^1_2 {} xrightarrow{mathbf{V} updownarrow} {} ^3_4 Box ^2_1 $$
The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).


You could also watch the matrices work on Mona step by step too, to help your intuition.
Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 overset{f}{longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg.  ) which is an "even"
) which is an "even"  stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other
stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.

$endgroup$
1
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
add a comment |
$begingroup$
By Flanigan & Kazdan:


Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)

This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 Box ^2_3 {} xrightarrow{mathbf{V} updownarrow} {} ^4_1 Box ^3_2 {} xrightarrow{Theta_{90} curvearrowright} {} ^1_2 Box ^4_3 $$ versus $$^1_4 Box ^2_3 {} xrightarrow{Theta_{90} curvearrowright} {} ^4_3 Box ^1_2 {} xrightarrow{mathbf{V} updownarrow} {} ^3_4 Box ^2_1 $$
The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).


You could also watch the matrices work on Mona step by step too, to help your intuition.
Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 overset{f}{longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg.  ) which is an "even"
) which is an "even"  stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other
stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.

$endgroup$
By Flanigan & Kazdan:


Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)

This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 Box ^2_3 {} xrightarrow{mathbf{V} updownarrow} {} ^4_1 Box ^3_2 {} xrightarrow{Theta_{90} curvearrowright} {} ^1_2 Box ^4_3 $$ versus $$^1_4 Box ^2_3 {} xrightarrow{Theta_{90} curvearrowright} {} ^4_3 Box ^1_2 {} xrightarrow{mathbf{V} updownarrow} {} ^3_4 Box ^2_1 $$
The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).


You could also watch the matrices work on Mona step by step too, to help your intuition.
Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 overset{f}{longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg.  ) which is an "even"
) which is an "even"  stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other
stretching/dilation. $$vec{y}=left[ mathbf{M} right] vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.

edited Feb 10 at 22:10
Glorfindel
3,41381830
3,41381830
answered Oct 3 '14 at 5:39
isomorphismesisomorphismes
2,45112744
2,45112744
1
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
add a comment |
1
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
1
1
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
$begingroup$
what happened to the captions for parts (e) and (f) of the kazdan graphic?
$endgroup$
– MichaelChirico
Oct 2 '16 at 0:54
add a comment |
$begingroup$
Apart from the interpretation as the composition of linear functions (which is, in my opinion, the most natural one), another viewpoint is on some occasions useful.
You can view them as something akin to a generalization of elementary row/column operations. If you compute $AB$, then the coefficients in $j$-th row of $A$ tell you, which linear combination of rows of B you should compute and put into the $j$-th row of the new matrix.
Similarly, you can view $AB$ as making linear combinations of columns of $A$, with the coefficients prescribed by the matrix $B$.
With this viewpoint in mind you can easily see that, if you denote by $vec{a}_1,dots,vec a_k$ the rows of the matrix $A$, then the equality
$$begin{pmatrix}vec a_1\vdots\vec a_kend{pmatrix}B=
begin{pmatrix}vec a_1B\vdots\vec a_kBend{pmatrix}$$
holds. (Of course, you can obtain this equality directly from definition or by many other methods. My intention was to illustrate a situation, when familiarity this viewpoint could be useful.)
$endgroup$
1
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
add a comment |
$begingroup$
Apart from the interpretation as the composition of linear functions (which is, in my opinion, the most natural one), another viewpoint is on some occasions useful.
You can view them as something akin to a generalization of elementary row/column operations. If you compute $AB$, then the coefficients in $j$-th row of $A$ tell you, which linear combination of rows of B you should compute and put into the $j$-th row of the new matrix.
Similarly, you can view $AB$ as making linear combinations of columns of $A$, with the coefficients prescribed by the matrix $B$.
With this viewpoint in mind you can easily see that, if you denote by $vec{a}_1,dots,vec a_k$ the rows of the matrix $A$, then the equality
$$begin{pmatrix}vec a_1\vdots\vec a_kend{pmatrix}B=
begin{pmatrix}vec a_1B\vdots\vec a_kBend{pmatrix}$$
holds. (Of course, you can obtain this equality directly from definition or by many other methods. My intention was to illustrate a situation, when familiarity this viewpoint could be useful.)
$endgroup$
1
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
add a comment |
$begingroup$
Apart from the interpretation as the composition of linear functions (which is, in my opinion, the most natural one), another viewpoint is on some occasions useful.
You can view them as something akin to a generalization of elementary row/column operations. If you compute $AB$, then the coefficients in $j$-th row of $A$ tell you, which linear combination of rows of B you should compute and put into the $j$-th row of the new matrix.
Similarly, you can view $AB$ as making linear combinations of columns of $A$, with the coefficients prescribed by the matrix $B$.
With this viewpoint in mind you can easily see that, if you denote by $vec{a}_1,dots,vec a_k$ the rows of the matrix $A$, then the equality
$$begin{pmatrix}vec a_1\vdots\vec a_kend{pmatrix}B=
begin{pmatrix}vec a_1B\vdots\vec a_kBend{pmatrix}$$
holds. (Of course, you can obtain this equality directly from definition or by many other methods. My intention was to illustrate a situation, when familiarity this viewpoint could be useful.)
$endgroup$
Apart from the interpretation as the composition of linear functions (which is, in my opinion, the most natural one), another viewpoint is on some occasions useful.
You can view them as something akin to a generalization of elementary row/column operations. If you compute $AB$, then the coefficients in $j$-th row of $A$ tell you, which linear combination of rows of B you should compute and put into the $j$-th row of the new matrix.
Similarly, you can view $AB$ as making linear combinations of columns of $A$, with the coefficients prescribed by the matrix $B$.
With this viewpoint in mind you can easily see that, if you denote by $vec{a}_1,dots,vec a_k$ the rows of the matrix $A$, then the equality
$$begin{pmatrix}vec a_1\vdots\vec a_kend{pmatrix}B=
begin{pmatrix}vec a_1B\vdots\vec a_kBend{pmatrix}$$
holds. (Of course, you can obtain this equality directly from definition or by many other methods. My intention was to illustrate a situation, when familiarity this viewpoint could be useful.)
edited Jan 5 '17 at 9:14
answered Apr 8 '11 at 13:28
Martin SleziakMartin Sleziak
44.9k10122277
44.9k10122277
1
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
add a comment |
1
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
1
1
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
$begingroup$
I came here to talk about composition of linear functions, or elementary row/column operations. But you already said it all. Great job, and +1 also you would deserve more.
$endgroup$
– Wok
Apr 8 '11 at 21:01
add a comment |
$begingroup$
First, Understand Vector multiplication by a scalar.
Then, think on a Matrix, multiplicated by a vector. The Matrix is a "vector of vectors".
Finally, Matrix X Matrix extends the former concept.
$endgroup$
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
1
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
1
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
add a comment |
$begingroup$
First, Understand Vector multiplication by a scalar.
Then, think on a Matrix, multiplicated by a vector. The Matrix is a "vector of vectors".
Finally, Matrix X Matrix extends the former concept.
$endgroup$
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
1
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
1
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
add a comment |
$begingroup$
First, Understand Vector multiplication by a scalar.
Then, think on a Matrix, multiplicated by a vector. The Matrix is a "vector of vectors".
Finally, Matrix X Matrix extends the former concept.
$endgroup$
First, Understand Vector multiplication by a scalar.
Then, think on a Matrix, multiplicated by a vector. The Matrix is a "vector of vectors".
Finally, Matrix X Matrix extends the former concept.
answered Apr 8 '11 at 22:56
Herman JungeHerman Junge
26114
26114
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
1
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
1
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
add a comment |
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
1
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
1
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
$begingroup$
This is a great answer. Now explained enough though. It is a similar way to how Gilbert Strang 'builds' up matrix multiplication in his video lectures.
$endgroup$
– Vass
May 18 '11 at 15:49
1
1
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
$begingroup$
This is the best answer so far as you do not need to know about transformations.
$endgroup$
– matqkks
Aug 6 '13 at 20:14
1
1
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
$begingroup$
The problem with this approach is to motivate the multiplication of a matrix by a vector.
$endgroup$
– Maxis Jaisi
May 19 '17 at 6:30
add a comment |
$begingroup$
Suppose
begin{align}
p & = 2x + 3y \
q & = 3x - 7y \
r & = -8x+9y
end{align}
Represent this way from transforming $begin{bmatrix} x \ y end{bmatrix}$ to $begin{bmatrix} p \ q \ r end{bmatrix}$ by the matrix
$$
left[begin{array}{rr} 2 & 3 \ 3 & -7 \ -8 & 9 end{array}right].
$$
Now let's transform $begin{bmatrix} p \ q \ r end{bmatrix}$ to $begin{bmatrix} a \ b end{bmatrix}$:
begin{align}
a & = 22p-38q+17r \
b & = 13p+10q+9r
end{align}
represent that by the matrix
$$
left[begin{array}{rr} 22 & -38 & 17 \ 13 & 10 & 9 end{array}right].
$$
So how do we transform $begin{bmatrix} x \ y end{bmatrix}$ directly to $begin{bmatrix} a \ b end{bmatrix}$?
Do a bit of algebra and you get
begin{align}
a & = bullet, x + bullet, y \
b & = bullet, x + bullet, y
end{align}
and you should be able to figure out what numbers the four $bullet$s are. That matrix of four $bullet$s is what you get when you multiply those earlier matrices. That's why matrix multiplication is defined the way it is.
$endgroup$
2
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
|
show 1 more comment
$begingroup$
Suppose
begin{align}
p & = 2x + 3y \
q & = 3x - 7y \
r & = -8x+9y
end{align}
Represent this way from transforming $begin{bmatrix} x \ y end{bmatrix}$ to $begin{bmatrix} p \ q \ r end{bmatrix}$ by the matrix
$$
left[begin{array}{rr} 2 & 3 \ 3 & -7 \ -8 & 9 end{array}right].
$$
Now let's transform $begin{bmatrix} p \ q \ r end{bmatrix}$ to $begin{bmatrix} a \ b end{bmatrix}$:
begin{align}
a & = 22p-38q+17r \
b & = 13p+10q+9r
end{align}
represent that by the matrix
$$
left[begin{array}{rr} 22 & -38 & 17 \ 13 & 10 & 9 end{array}right].
$$
So how do we transform $begin{bmatrix} x \ y end{bmatrix}$ directly to $begin{bmatrix} a \ b end{bmatrix}$?
Do a bit of algebra and you get
begin{align}
a & = bullet, x + bullet, y \
b & = bullet, x + bullet, y
end{align}
and you should be able to figure out what numbers the four $bullet$s are. That matrix of four $bullet$s is what you get when you multiply those earlier matrices. That's why matrix multiplication is defined the way it is.
$endgroup$
2
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
|
show 1 more comment
$begingroup$
Suppose
begin{align}
p & = 2x + 3y \
q & = 3x - 7y \
r & = -8x+9y
end{align}
Represent this way from transforming $begin{bmatrix} x \ y end{bmatrix}$ to $begin{bmatrix} p \ q \ r end{bmatrix}$ by the matrix
$$
left[begin{array}{rr} 2 & 3 \ 3 & -7 \ -8 & 9 end{array}right].
$$
Now let's transform $begin{bmatrix} p \ q \ r end{bmatrix}$ to $begin{bmatrix} a \ b end{bmatrix}$:
begin{align}
a & = 22p-38q+17r \
b & = 13p+10q+9r
end{align}
represent that by the matrix
$$
left[begin{array}{rr} 22 & -38 & 17 \ 13 & 10 & 9 end{array}right].
$$
So how do we transform $begin{bmatrix} x \ y end{bmatrix}$ directly to $begin{bmatrix} a \ b end{bmatrix}$?
Do a bit of algebra and you get
begin{align}
a & = bullet, x + bullet, y \
b & = bullet, x + bullet, y
end{align}
and you should be able to figure out what numbers the four $bullet$s are. That matrix of four $bullet$s is what you get when you multiply those earlier matrices. That's why matrix multiplication is defined the way it is.
$endgroup$
Suppose
begin{align}
p & = 2x + 3y \
q & = 3x - 7y \
r & = -8x+9y
end{align}
Represent this way from transforming $begin{bmatrix} x \ y end{bmatrix}$ to $begin{bmatrix} p \ q \ r end{bmatrix}$ by the matrix
$$
left[begin{array}{rr} 2 & 3 \ 3 & -7 \ -8 & 9 end{array}right].
$$
Now let's transform $begin{bmatrix} p \ q \ r end{bmatrix}$ to $begin{bmatrix} a \ b end{bmatrix}$:
begin{align}
a & = 22p-38q+17r \
b & = 13p+10q+9r
end{align}
represent that by the matrix
$$
left[begin{array}{rr} 22 & -38 & 17 \ 13 & 10 & 9 end{array}right].
$$
So how do we transform $begin{bmatrix} x \ y end{bmatrix}$ directly to $begin{bmatrix} a \ b end{bmatrix}$?
Do a bit of algebra and you get
begin{align}
a & = bullet, x + bullet, y \
b & = bullet, x + bullet, y
end{align}
and you should be able to figure out what numbers the four $bullet$s are. That matrix of four $bullet$s is what you get when you multiply those earlier matrices. That's why matrix multiplication is defined the way it is.
edited Jul 14 '15 at 20:13
answered Jul 7 '13 at 21:06
Michael HardyMichael Hardy
1
1
2
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
|
show 1 more comment
2
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
2
2
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
Perhaps a link to the other answer with some explanation of how it applies to this problem would be better than duplicating an answer. This meta question, and those cited therein, is a good discussion of the concerns.
$endgroup$
– robjohn♦
Jul 8 '13 at 14:22
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I like this answer. As linear algebra is really about linear systems so this answer fits in with that definition of linear algebra.
$endgroup$
– matqkks
Aug 6 '13 at 20:16
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
I'm stuck on how a=22p−38q+17r and b=13p+10q+9r are obtained. If you wish to explain this I'd really appreciate.
$endgroup$
– Paolo
Jun 27 '14 at 15:28
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
@Guandalino : It was not "obtained"; rather it is part of that from which one obtains something else, where the four $bullet$s appear.
$endgroup$
– Michael Hardy
Jun 27 '14 at 16:38
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
$begingroup$
Apologies for not being clear. My question is, how the numbers 22, -38, 17, 13, 10, and 9 get calculated?
$endgroup$
– Paolo
Jun 27 '14 at 18:34
|
show 1 more comment
$begingroup$
To get away from how these two kinds of multiplications are implemented (repeated addition for numbers vs. row/column dot product for matrices) and how they behave symbolically/algebraically (associativity, distribute over 'addition', have annihilators, etc), I'd like to answer in the manner 'what are they good for?'
Multiplication of numbers gives area of a rectangle with sides given by the multiplicands (or number of total points if thinking discretely).
Multiplication of matrices (since it involves quite a few more actual numbers than just simple multiplication) is understandably quite a bit more complex. Though the composition of linear functions (as mentioned elsewhere) is the essence of it, that's not the most intuitive description of it (to someone without the abstract algebraic experience). A more visual intuition is that one matrix, multiplying with another, results in the transformation of a set of points (the columns of the right-hand matrix) into new set of points (the columns of the resulting matrix). That is, take a set of $n$ points in $n$ dimensions, put them as columns in an $ntimes n$ matrix; if you multiply this from the left by another $n times n$ matrix, you'll transform that 'cloud' of points to a new cloud.
This transformation isn't some random thing; it might rotate the cloud, it might expand the cloud, it won't 'translate' the cloud, it might collapse the cloud into a line (a lower number of dimensions might be needed). But it's transforming the whole cloud all at once smoothly (near points get translated to near points).
So that is one way of getting the 'meaning' of matrix multiplication.
I have a hard time getting a good metaphor (any metaphor) between matrix multiplication and simple numerical multiplication so I won't force it - hopefully someone else might be able to come up with a better visualization that shows how they're more alike beyond the similarity of some algebraic properties.
$endgroup$
add a comment |
$begingroup$
To get away from how these two kinds of multiplications are implemented (repeated addition for numbers vs. row/column dot product for matrices) and how they behave symbolically/algebraically (associativity, distribute over 'addition', have annihilators, etc), I'd like to answer in the manner 'what are they good for?'
Multiplication of numbers gives area of a rectangle with sides given by the multiplicands (or number of total points if thinking discretely).
Multiplication of matrices (since it involves quite a few more actual numbers than just simple multiplication) is understandably quite a bit more complex. Though the composition of linear functions (as mentioned elsewhere) is the essence of it, that's not the most intuitive description of it (to someone without the abstract algebraic experience). A more visual intuition is that one matrix, multiplying with another, results in the transformation of a set of points (the columns of the right-hand matrix) into new set of points (the columns of the resulting matrix). That is, take a set of $n$ points in $n$ dimensions, put them as columns in an $ntimes n$ matrix; if you multiply this from the left by another $n times n$ matrix, you'll transform that 'cloud' of points to a new cloud.
This transformation isn't some random thing; it might rotate the cloud, it might expand the cloud, it won't 'translate' the cloud, it might collapse the cloud into a line (a lower number of dimensions might be needed). But it's transforming the whole cloud all at once smoothly (near points get translated to near points).
So that is one way of getting the 'meaning' of matrix multiplication.
I have a hard time getting a good metaphor (any metaphor) between matrix multiplication and simple numerical multiplication so I won't force it - hopefully someone else might be able to come up with a better visualization that shows how they're more alike beyond the similarity of some algebraic properties.
$endgroup$
add a comment |
$begingroup$
To get away from how these two kinds of multiplications are implemented (repeated addition for numbers vs. row/column dot product for matrices) and how they behave symbolically/algebraically (associativity, distribute over 'addition', have annihilators, etc), I'd like to answer in the manner 'what are they good for?'
Multiplication of numbers gives area of a rectangle with sides given by the multiplicands (or number of total points if thinking discretely).
Multiplication of matrices (since it involves quite a few more actual numbers than just simple multiplication) is understandably quite a bit more complex. Though the composition of linear functions (as mentioned elsewhere) is the essence of it, that's not the most intuitive description of it (to someone without the abstract algebraic experience). A more visual intuition is that one matrix, multiplying with another, results in the transformation of a set of points (the columns of the right-hand matrix) into new set of points (the columns of the resulting matrix). That is, take a set of $n$ points in $n$ dimensions, put them as columns in an $ntimes n$ matrix; if you multiply this from the left by another $n times n$ matrix, you'll transform that 'cloud' of points to a new cloud.
This transformation isn't some random thing; it might rotate the cloud, it might expand the cloud, it won't 'translate' the cloud, it might collapse the cloud into a line (a lower number of dimensions might be needed). But it's transforming the whole cloud all at once smoothly (near points get translated to near points).
So that is one way of getting the 'meaning' of matrix multiplication.
I have a hard time getting a good metaphor (any metaphor) between matrix multiplication and simple numerical multiplication so I won't force it - hopefully someone else might be able to come up with a better visualization that shows how they're more alike beyond the similarity of some algebraic properties.
$endgroup$
To get away from how these two kinds of multiplications are implemented (repeated addition for numbers vs. row/column dot product for matrices) and how they behave symbolically/algebraically (associativity, distribute over 'addition', have annihilators, etc), I'd like to answer in the manner 'what are they good for?'
Multiplication of numbers gives area of a rectangle with sides given by the multiplicands (or number of total points if thinking discretely).
Multiplication of matrices (since it involves quite a few more actual numbers than just simple multiplication) is understandably quite a bit more complex. Though the composition of linear functions (as mentioned elsewhere) is the essence of it, that's not the most intuitive description of it (to someone without the abstract algebraic experience). A more visual intuition is that one matrix, multiplying with another, results in the transformation of a set of points (the columns of the right-hand matrix) into new set of points (the columns of the resulting matrix). That is, take a set of $n$ points in $n$ dimensions, put them as columns in an $ntimes n$ matrix; if you multiply this from the left by another $n times n$ matrix, you'll transform that 'cloud' of points to a new cloud.
This transformation isn't some random thing; it might rotate the cloud, it might expand the cloud, it won't 'translate' the cloud, it might collapse the cloud into a line (a lower number of dimensions might be needed). But it's transforming the whole cloud all at once smoothly (near points get translated to near points).
So that is one way of getting the 'meaning' of matrix multiplication.
I have a hard time getting a good metaphor (any metaphor) between matrix multiplication and simple numerical multiplication so I won't force it - hopefully someone else might be able to come up with a better visualization that shows how they're more alike beyond the similarity of some algebraic properties.
edited Sep 17 '15 at 13:13
answered Apr 8 '11 at 20:53
MitchMitch
6,0772560
6,0772560
add a comment |
add a comment |
$begingroup$
You shouldn't try to think in terms of scalars and try to fit matrices into this way of thinking.
It's exactly like with real and complex numbers. It's difficult to have an intuition about complex operations if you try to think in terms of real operations.
scalars are a special case of matrices, as real numbers are a special case of complex numbers.
So you need to look at it from the other, more abstract side. If you think about real operations in terms of complex operations, they make complete sense (they are a simple case of the complex operations).
And the same is true for Matrices and scalars. Think in terms of matrix operations and you will see that the scalar operations are a simple (special) case of the corresponding matrix operations.
$endgroup$
add a comment |
$begingroup$
You shouldn't try to think in terms of scalars and try to fit matrices into this way of thinking.
It's exactly like with real and complex numbers. It's difficult to have an intuition about complex operations if you try to think in terms of real operations.
scalars are a special case of matrices, as real numbers are a special case of complex numbers.
So you need to look at it from the other, more abstract side. If you think about real operations in terms of complex operations, they make complete sense (they are a simple case of the complex operations).
And the same is true for Matrices and scalars. Think in terms of matrix operations and you will see that the scalar operations are a simple (special) case of the corresponding matrix operations.
$endgroup$
add a comment |
$begingroup$
You shouldn't try to think in terms of scalars and try to fit matrices into this way of thinking.
It's exactly like with real and complex numbers. It's difficult to have an intuition about complex operations if you try to think in terms of real operations.
scalars are a special case of matrices, as real numbers are a special case of complex numbers.
So you need to look at it from the other, more abstract side. If you think about real operations in terms of complex operations, they make complete sense (they are a simple case of the complex operations).
And the same is true for Matrices and scalars. Think in terms of matrix operations and you will see that the scalar operations are a simple (special) case of the corresponding matrix operations.
$endgroup$
You shouldn't try to think in terms of scalars and try to fit matrices into this way of thinking.
It's exactly like with real and complex numbers. It's difficult to have an intuition about complex operations if you try to think in terms of real operations.
scalars are a special case of matrices, as real numbers are a special case of complex numbers.
So you need to look at it from the other, more abstract side. If you think about real operations in terms of complex operations, they make complete sense (they are a simple case of the complex operations).
And the same is true for Matrices and scalars. Think in terms of matrix operations and you will see that the scalar operations are a simple (special) case of the corresponding matrix operations.
edited Feb 21 '16 at 23:24
John B
12.3k51840
12.3k51840
answered Apr 8 '11 at 17:38
user9310
add a comment |
add a comment |
$begingroup$
One way to try to "understand" it would be to think of two factors in the product of two numbers as two different entities: one is multiplying and the other is being multiplied. For example, in $5cdot4$, $5$ is the one that is multiplying $4$, and $4$ is being multiplied by $5$. You can think in terms of repetitive addition that you are adding $4$ to itself $5$ times: You are doing something to $4$ to get another number, that something is characterized by the number $5$. We forbid the interpretation that you are adding $5$ to itself $4$ times here, because $5cdot$ is an action that is related to the number $5$, it is not a number. Now, what happens if you multiply $4$ by $5$, and then multiply the result by $3$? In other words,
$3cdot(5cdot4)=?$
or more generally,
$3cdot(5cdot x)=?$
when we want to vary the number being multiplied. Think of for example, we need to multiply a lot of different numbers $x$ by $5$ first and then by $3$, and we want to somehow simplify this process, or to find a way to compute this operation fast.
Without going into the details, we all know the above is equal to
$3cdot(5cdot x)=(3times 5)cdot x$,
where
$3times 5$ is just the ordinary product of two numbers, but I used different notation to emphasize that this time we are multiplying "multipliers" together, meaning that the result of this operation is an entity that multiplies other numbers, in contrast to the result of $5cdot4$, which is an entity that gets multiplied. Note that in some sense, in $3times5$ the numbers $5$ and $3$ participates on an equal ground, while in $5cdot4$ the numbers have differing roles. For the operation $times$ no interpretation is available in terms of repetitive addition, because we have two actions, not an action and a number. In linear algebra, the entities that gets multiplied are vectors, the "multiplier" objects are matrices, the operation $cdot$ generalizes to the matrix-vector product, and the operation $times$ extends to the product between matrices.
$endgroup$
add a comment |
$begingroup$
One way to try to "understand" it would be to think of two factors in the product of two numbers as two different entities: one is multiplying and the other is being multiplied. For example, in $5cdot4$, $5$ is the one that is multiplying $4$, and $4$ is being multiplied by $5$. You can think in terms of repetitive addition that you are adding $4$ to itself $5$ times: You are doing something to $4$ to get another number, that something is characterized by the number $5$. We forbid the interpretation that you are adding $5$ to itself $4$ times here, because $5cdot$ is an action that is related to the number $5$, it is not a number. Now, what happens if you multiply $4$ by $5$, and then multiply the result by $3$? In other words,
$3cdot(5cdot4)=?$
or more generally,
$3cdot(5cdot x)=?$
when we want to vary the number being multiplied. Think of for example, we need to multiply a lot of different numbers $x$ by $5$ first and then by $3$, and we want to somehow simplify this process, or to find a way to compute this operation fast.
Without going into the details, we all know the above is equal to
$3cdot(5cdot x)=(3times 5)cdot x$,
where
$3times 5$ is just the ordinary product of two numbers, but I used different notation to emphasize that this time we are multiplying "multipliers" together, meaning that the result of this operation is an entity that multiplies other numbers, in contrast to the result of $5cdot4$, which is an entity that gets multiplied. Note that in some sense, in $3times5$ the numbers $5$ and $3$ participates on an equal ground, while in $5cdot4$ the numbers have differing roles. For the operation $times$ no interpretation is available in terms of repetitive addition, because we have two actions, not an action and a number. In linear algebra, the entities that gets multiplied are vectors, the "multiplier" objects are matrices, the operation $cdot$ generalizes to the matrix-vector product, and the operation $times$ extends to the product between matrices.
$endgroup$
add a comment |
$begingroup$
One way to try to "understand" it would be to think of two factors in the product of two numbers as two different entities: one is multiplying and the other is being multiplied. For example, in $5cdot4$, $5$ is the one that is multiplying $4$, and $4$ is being multiplied by $5$. You can think in terms of repetitive addition that you are adding $4$ to itself $5$ times: You are doing something to $4$ to get another number, that something is characterized by the number $5$. We forbid the interpretation that you are adding $5$ to itself $4$ times here, because $5cdot$ is an action that is related to the number $5$, it is not a number. Now, what happens if you multiply $4$ by $5$, and then multiply the result by $3$? In other words,
$3cdot(5cdot4)=?$
or more generally,
$3cdot(5cdot x)=?$
when we want to vary the number being multiplied. Think of for example, we need to multiply a lot of different numbers $x$ by $5$ first and then by $3$, and we want to somehow simplify this process, or to find a way to compute this operation fast.
Without going into the details, we all know the above is equal to
$3cdot(5cdot x)=(3times 5)cdot x$,
where
$3times 5$ is just the ordinary product of two numbers, but I used different notation to emphasize that this time we are multiplying "multipliers" together, meaning that the result of this operation is an entity that multiplies other numbers, in contrast to the result of $5cdot4$, which is an entity that gets multiplied. Note that in some sense, in $3times5$ the numbers $5$ and $3$ participates on an equal ground, while in $5cdot4$ the numbers have differing roles. For the operation $times$ no interpretation is available in terms of repetitive addition, because we have two actions, not an action and a number. In linear algebra, the entities that gets multiplied are vectors, the "multiplier" objects are matrices, the operation $cdot$ generalizes to the matrix-vector product, and the operation $times$ extends to the product between matrices.
$endgroup$
One way to try to "understand" it would be to think of two factors in the product of two numbers as two different entities: one is multiplying and the other is being multiplied. For example, in $5cdot4$, $5$ is the one that is multiplying $4$, and $4$ is being multiplied by $5$. You can think in terms of repetitive addition that you are adding $4$ to itself $5$ times: You are doing something to $4$ to get another number, that something is characterized by the number $5$. We forbid the interpretation that you are adding $5$ to itself $4$ times here, because $5cdot$ is an action that is related to the number $5$, it is not a number. Now, what happens if you multiply $4$ by $5$, and then multiply the result by $3$? In other words,
$3cdot(5cdot4)=?$
or more generally,
$3cdot(5cdot x)=?$
when we want to vary the number being multiplied. Think of for example, we need to multiply a lot of different numbers $x$ by $5$ first and then by $3$, and we want to somehow simplify this process, or to find a way to compute this operation fast.
Without going into the details, we all know the above is equal to
$3cdot(5cdot x)=(3times 5)cdot x$,
where
$3times 5$ is just the ordinary product of two numbers, but I used different notation to emphasize that this time we are multiplying "multipliers" together, meaning that the result of this operation is an entity that multiplies other numbers, in contrast to the result of $5cdot4$, which is an entity that gets multiplied. Note that in some sense, in $3times5$ the numbers $5$ and $3$ participates on an equal ground, while in $5cdot4$ the numbers have differing roles. For the operation $times$ no interpretation is available in terms of repetitive addition, because we have two actions, not an action and a number. In linear algebra, the entities that gets multiplied are vectors, the "multiplier" objects are matrices, the operation $cdot$ generalizes to the matrix-vector product, and the operation $times$ extends to the product between matrices.
edited Apr 8 '11 at 18:13
answered Apr 8 '11 at 17:57
timurtimur
12.2k2144
12.2k2144
add a comment |
add a comment |
$begingroup$
Let's say you're multiplying matrix $A$ by matrix $B$ and producing $C$:
$A times B = C$
At a high level, $A$ represents a set of linear functions or transformations to apply, $B$ is a set of values for the input variables to run through the linear functions/transformations, and $C$ is the result of applying the linear functions/transformations to the input values.
For more details, see below:
(1) $A$ consists of rows, each of which corresponds to a linear function/transformation
For instance, let's say the first row in $A$ is $[a_1 , a_2 , a_3]$ where $a_1$, $a_2$ and $a_3$ are constants. Such row corresponds to the linear function/transformation:
$$f(x, y, z) = a_1x + a_2y + a_3z$$
(2) $B$ consists of columns, each of which corresponds to values for the input variables.
For instance, let's say the first column in $B$ consists of the values $[b_1 , b_2 , b_3]$ (transpose). Such column correspond to setting the input variable values as follows:
$$x=b_1 \ y=b_2 \ z=b_3$$
(3) $C$ consists of entries whereby an entry at row $i$ and column $j$ corresponds to applying the linear function/transformation represented in $A$'s $i$th row to the input variable values provided by $B$'s $j$th column.
Thus, the entry in the first row and first column of $C$ in the example discussed thus far, would equate to:
begin{align}
f(x=b_1, y=b_2, z=b_3) &= a_1x + a_2y + a_3z \
&= a_1b_1 + a_2b_2 + a_3b_3
end{align}
$endgroup$
add a comment |
$begingroup$
Let's say you're multiplying matrix $A$ by matrix $B$ and producing $C$:
$A times B = C$
At a high level, $A$ represents a set of linear functions or transformations to apply, $B$ is a set of values for the input variables to run through the linear functions/transformations, and $C$ is the result of applying the linear functions/transformations to the input values.
For more details, see below:
(1) $A$ consists of rows, each of which corresponds to a linear function/transformation
For instance, let's say the first row in $A$ is $[a_1 , a_2 , a_3]$ where $a_1$, $a_2$ and $a_3$ are constants. Such row corresponds to the linear function/transformation:
$$f(x, y, z) = a_1x + a_2y + a_3z$$
(2) $B$ consists of columns, each of which corresponds to values for the input variables.
For instance, let's say the first column in $B$ consists of the values $[b_1 , b_2 , b_3]$ (transpose). Such column correspond to setting the input variable values as follows:
$$x=b_1 \ y=b_2 \ z=b_3$$
(3) $C$ consists of entries whereby an entry at row $i$ and column $j$ corresponds to applying the linear function/transformation represented in $A$'s $i$th row to the input variable values provided by $B$'s $j$th column.
Thus, the entry in the first row and first column of $C$ in the example discussed thus far, would equate to:
begin{align}
f(x=b_1, y=b_2, z=b_3) &= a_1x + a_2y + a_3z \
&= a_1b_1 + a_2b_2 + a_3b_3
end{align}
$endgroup$
add a comment |
$begingroup$
Let's say you're multiplying matrix $A$ by matrix $B$ and producing $C$:
$A times B = C$
At a high level, $A$ represents a set of linear functions or transformations to apply, $B$ is a set of values for the input variables to run through the linear functions/transformations, and $C$ is the result of applying the linear functions/transformations to the input values.
For more details, see below:
(1) $A$ consists of rows, each of which corresponds to a linear function/transformation
For instance, let's say the first row in $A$ is $[a_1 , a_2 , a_3]$ where $a_1$, $a_2$ and $a_3$ are constants. Such row corresponds to the linear function/transformation:
$$f(x, y, z) = a_1x + a_2y + a_3z$$
(2) $B$ consists of columns, each of which corresponds to values for the input variables.
For instance, let's say the first column in $B$ consists of the values $[b_1 , b_2 , b_3]$ (transpose). Such column correspond to setting the input variable values as follows:
$$x=b_1 \ y=b_2 \ z=b_3$$
(3) $C$ consists of entries whereby an entry at row $i$ and column $j$ corresponds to applying the linear function/transformation represented in $A$'s $i$th row to the input variable values provided by $B$'s $j$th column.
Thus, the entry in the first row and first column of $C$ in the example discussed thus far, would equate to:
begin{align}
f(x=b_1, y=b_2, z=b_3) &= a_1x + a_2y + a_3z \
&= a_1b_1 + a_2b_2 + a_3b_3
end{align}
$endgroup$
Let's say you're multiplying matrix $A$ by matrix $B$ and producing $C$:
$A times B = C$
At a high level, $A$ represents a set of linear functions or transformations to apply, $B$ is a set of values for the input variables to run through the linear functions/transformations, and $C$ is the result of applying the linear functions/transformations to the input values.
For more details, see below:
(1) $A$ consists of rows, each of which corresponds to a linear function/transformation
For instance, let's say the first row in $A$ is $[a_1 , a_2 , a_3]$ where $a_1$, $a_2$ and $a_3$ are constants. Such row corresponds to the linear function/transformation:
$$f(x, y, z) = a_1x + a_2y + a_3z$$
(2) $B$ consists of columns, each of which corresponds to values for the input variables.
For instance, let's say the first column in $B$ consists of the values $[b_1 , b_2 , b_3]$ (transpose). Such column correspond to setting the input variable values as follows:
$$x=b_1 \ y=b_2 \ z=b_3$$
(3) $C$ consists of entries whereby an entry at row $i$ and column $j$ corresponds to applying the linear function/transformation represented in $A$'s $i$th row to the input variable values provided by $B$'s $j$th column.
Thus, the entry in the first row and first column of $C$ in the example discussed thus far, would equate to:
begin{align}
f(x=b_1, y=b_2, z=b_3) &= a_1x + a_2y + a_3z \
&= a_1b_1 + a_2b_2 + a_3b_3
end{align}
edited Oct 2 '16 at 1:01
MichaelChirico
3,5381126
3,5381126
answered Oct 21 '15 at 19:57
blublu
111
111
add a comment |
add a comment |
$begingroup$
Instead of trying to explain it, I will link you to an interactive graphic. As you play around with it, watch how the matrix in the top left corner changes as you move X' and Y'. The intuition for how matrix multiplication works comes after the intuition for where it's used. https://www.geogebra.org/m/VjhNaB8V
$endgroup$
add a comment |
$begingroup$
Instead of trying to explain it, I will link you to an interactive graphic. As you play around with it, watch how the matrix in the top left corner changes as you move X' and Y'. The intuition for how matrix multiplication works comes after the intuition for where it's used. https://www.geogebra.org/m/VjhNaB8V
$endgroup$
add a comment |
$begingroup$
Instead of trying to explain it, I will link you to an interactive graphic. As you play around with it, watch how the matrix in the top left corner changes as you move X' and Y'. The intuition for how matrix multiplication works comes after the intuition for where it's used. https://www.geogebra.org/m/VjhNaB8V
$endgroup$
Instead of trying to explain it, I will link you to an interactive graphic. As you play around with it, watch how the matrix in the top left corner changes as you move X' and Y'. The intuition for how matrix multiplication works comes after the intuition for where it's used. https://www.geogebra.org/m/VjhNaB8V
answered May 10 '17 at 12:25
Nathan PetrangeloNathan Petrangelo
1
1
add a comment |
add a comment |
$begingroup$
Let's explain where matrices and matrix multiplication come from. But first a bit of notation: $e_i$ denotes the column vector in $mathbb R^n$ which has a 1 in the $i$th position and zeros elsewhere:
$$
e_1 = begin{bmatrix} 1 \ 0 \ 0 \ vdots \ 0 end{bmatrix},
e_2 = begin{bmatrix} 0 \ 1 \ 0 \ vdots \ 0 end{bmatrix},
ldots,
e_n = begin{bmatrix} 0 \ 0 \ 0 \ vdots \ 1 end{bmatrix}
.
$$
Suppose that $T:mathbb R^n to mathbb R^m$ is a linear transformation.
The matrix
$$
A = begin{bmatrix} T(e_1) & cdots & T(e_n) end{bmatrix}
$$
is called the matrix description of $T$.
If we are given $A$, then we can easily compute $T(x)$ for any vector $x in mathbb R^n$, as follows: If
$$
x = begin{bmatrix} x_1 \ vdots \ x_n end{bmatrix}
$$
then
$$
tag{1}T(x) = T(x_1 e_1 + cdots + x_n e_n) = x_1 underbrace{T(e_1)}_{text{known}} + cdots + x_n underbrace{T(e_n)}_{text{known}}.
$$
In other words, $T(x)$ is a linear combination of the columns of $A$. To save writing, we will denote this particular linear combination as $Ax$:
$$
Ax = x_1 cdot left(text{first column of $A$}right) + x_2 cdot left(text{second column of $A$}right) + cdots + x_n cdot left(text{final column of $A$} right).
$$
With this notation, equation (1) can be written as
$$
T(x) = Ax.
$$
Now suppose that $T:mathbb R^n to mathbb R^m$ and $S:mathbb R^m to mathbb R^p$ are linear transformations, and that $T$ and $S$ are represented by the matrices $A$ and $B$ respectively.
Let $a_i$ be the $i$th column of $A$.
Question: What is the matrix description of $S circ T$?
Answer: If $C$ is the matrix description of $S circ T$, then the $i$th column of $C$ is
begin{align}
c_i &= (S circ T)(e_i) \
&= S(T(e_i)) \
&= S(a_i) \
&= B a_i.
end{align}
For this reason, we define the "product" of $B$ and $A$ to be the matrix whose $i$th column is $B a_i$. With this notation, the matrix description of $S circ T$ is
$$
C = BA.
$$
If you write everything out in terms of components, you will observe that this definition agrees with the usual definition of matrix multiplication.
That is how matrices and matrix multiplication can be discovered.
$endgroup$
add a comment |
$begingroup$
Let's explain where matrices and matrix multiplication come from. But first a bit of notation: $e_i$ denotes the column vector in $mathbb R^n$ which has a 1 in the $i$th position and zeros elsewhere:
$$
e_1 = begin{bmatrix} 1 \ 0 \ 0 \ vdots \ 0 end{bmatrix},
e_2 = begin{bmatrix} 0 \ 1 \ 0 \ vdots \ 0 end{bmatrix},
ldots,
e_n = begin{bmatrix} 0 \ 0 \ 0 \ vdots \ 1 end{bmatrix}
.
$$
Suppose that $T:mathbb R^n to mathbb R^m$ is a linear transformation.
The matrix
$$
A = begin{bmatrix} T(e_1) & cdots & T(e_n) end{bmatrix}
$$
is called the matrix description of $T$.
If we are given $A$, then we can easily compute $T(x)$ for any vector $x in mathbb R^n$, as follows: If
$$
x = begin{bmatrix} x_1 \ vdots \ x_n end{bmatrix}
$$
then
$$
tag{1}T(x) = T(x_1 e_1 + cdots + x_n e_n) = x_1 underbrace{T(e_1)}_{text{known}} + cdots + x_n underbrace{T(e_n)}_{text{known}}.
$$
In other words, $T(x)$ is a linear combination of the columns of $A$. To save writing, we will denote this particular linear combination as $Ax$:
$$
Ax = x_1 cdot left(text{first column of $A$}right) + x_2 cdot left(text{second column of $A$}right) + cdots + x_n cdot left(text{final column of $A$} right).
$$
With this notation, equation (1) can be written as
$$
T(x) = Ax.
$$
Now suppose that $T:mathbb R^n to mathbb R^m$ and $S:mathbb R^m to mathbb R^p$ are linear transformations, and that $T$ and $S$ are represented by the matrices $A$ and $B$ respectively.
Let $a_i$ be the $i$th column of $A$.
Question: What is the matrix description of $S circ T$?
Answer: If $C$ is the matrix description of $S circ T$, then the $i$th column of $C$ is
begin{align}
c_i &= (S circ T)(e_i) \
&= S(T(e_i)) \
&= S(a_i) \
&= B a_i.
end{align}
For this reason, we define the "product" of $B$ and $A$ to be the matrix whose $i$th column is $B a_i$. With this notation, the matrix description of $S circ T$ is
$$
C = BA.
$$
If you write everything out in terms of components, you will observe that this definition agrees with the usual definition of matrix multiplication.
That is how matrices and matrix multiplication can be discovered.
$endgroup$
add a comment |
$begingroup$
Let's explain where matrices and matrix multiplication come from. But first a bit of notation: $e_i$ denotes the column vector in $mathbb R^n$ which has a 1 in the $i$th position and zeros elsewhere:
$$
e_1 = begin{bmatrix} 1 \ 0 \ 0 \ vdots \ 0 end{bmatrix},
e_2 = begin{bmatrix} 0 \ 1 \ 0 \ vdots \ 0 end{bmatrix},
ldots,
e_n = begin{bmatrix} 0 \ 0 \ 0 \ vdots \ 1 end{bmatrix}
.
$$
Suppose that $T:mathbb R^n to mathbb R^m$ is a linear transformation.
The matrix
$$
A = begin{bmatrix} T(e_1) & cdots & T(e_n) end{bmatrix}
$$
is called the matrix description of $T$.
If we are given $A$, then we can easily compute $T(x)$ for any vector $x in mathbb R^n$, as follows: If
$$
x = begin{bmatrix} x_1 \ vdots \ x_n end{bmatrix}
$$
then
$$
tag{1}T(x) = T(x_1 e_1 + cdots + x_n e_n) = x_1 underbrace{T(e_1)}_{text{known}} + cdots + x_n underbrace{T(e_n)}_{text{known}}.
$$
In other words, $T(x)$ is a linear combination of the columns of $A$. To save writing, we will denote this particular linear combination as $Ax$:
$$
Ax = x_1 cdot left(text{first column of $A$}right) + x_2 cdot left(text{second column of $A$}right) + cdots + x_n cdot left(text{final column of $A$} right).
$$
With this notation, equation (1) can be written as
$$
T(x) = Ax.
$$
Now suppose that $T:mathbb R^n to mathbb R^m$ and $S:mathbb R^m to mathbb R^p$ are linear transformations, and that $T$ and $S$ are represented by the matrices $A$ and $B$ respectively.
Let $a_i$ be the $i$th column of $A$.
Question: What is the matrix description of $S circ T$?
Answer: If $C$ is the matrix description of $S circ T$, then the $i$th column of $C$ is
begin{align}
c_i &= (S circ T)(e_i) \
&= S(T(e_i)) \
&= S(a_i) \
&= B a_i.
end{align}
For this reason, we define the "product" of $B$ and $A$ to be the matrix whose $i$th column is $B a_i$. With this notation, the matrix description of $S circ T$ is
$$
C = BA.
$$
If you write everything out in terms of components, you will observe that this definition agrees with the usual definition of matrix multiplication.
That is how matrices and matrix multiplication can be discovered.
$endgroup$
Let's explain where matrices and matrix multiplication come from. But first a bit of notation: $e_i$ denotes the column vector in $mathbb R^n$ which has a 1 in the $i$th position and zeros elsewhere:
$$
e_1 = begin{bmatrix} 1 \ 0 \ 0 \ vdots \ 0 end{bmatrix},
e_2 = begin{bmatrix} 0 \ 1 \ 0 \ vdots \ 0 end{bmatrix},
ldots,
e_n = begin{bmatrix} 0 \ 0 \ 0 \ vdots \ 1 end{bmatrix}
.
$$
Suppose that $T:mathbb R^n to mathbb R^m$ is a linear transformation.
The matrix
$$
A = begin{bmatrix} T(e_1) & cdots & T(e_n) end{bmatrix}
$$
is called the matrix description of $T$.
If we are given $A$, then we can easily compute $T(x)$ for any vector $x in mathbb R^n$, as follows: If
$$
x = begin{bmatrix} x_1 \ vdots \ x_n end{bmatrix}
$$
then
$$
tag{1}T(x) = T(x_1 e_1 + cdots + x_n e_n) = x_1 underbrace{T(e_1)}_{text{known}} + cdots + x_n underbrace{T(e_n)}_{text{known}}.
$$
In other words, $T(x)$ is a linear combination of the columns of $A$. To save writing, we will denote this particular linear combination as $Ax$:
$$
Ax = x_1 cdot left(text{first column of $A$}right) + x_2 cdot left(text{second column of $A$}right) + cdots + x_n cdot left(text{final column of $A$} right).
$$
With this notation, equation (1) can be written as
$$
T(x) = Ax.
$$
Now suppose that $T:mathbb R^n to mathbb R^m$ and $S:mathbb R^m to mathbb R^p$ are linear transformations, and that $T$ and $S$ are represented by the matrices $A$ and $B$ respectively.
Let $a_i$ be the $i$th column of $A$.
Question: What is the matrix description of $S circ T$?
Answer: If $C$ is the matrix description of $S circ T$, then the $i$th column of $C$ is
begin{align}
c_i &= (S circ T)(e_i) \
&= S(T(e_i)) \
&= S(a_i) \
&= B a_i.
end{align}
For this reason, we define the "product" of $B$ and $A$ to be the matrix whose $i$th column is $B a_i$. With this notation, the matrix description of $S circ T$ is
$$
C = BA.
$$
If you write everything out in terms of components, you will observe that this definition agrees with the usual definition of matrix multiplication.
That is how matrices and matrix multiplication can be discovered.
answered Dec 24 '18 at 7:21
littleOlittleO
30.3k648111
30.3k648111
add a comment |
add a comment |
$begingroup$
This is the detailed and easiest explanation : https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
$endgroup$
add a comment |
$begingroup$
This is the detailed and easiest explanation : https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
$endgroup$
add a comment |
$begingroup$
This is the detailed and easiest explanation : https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
$endgroup$
This is the detailed and easiest explanation : https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
answered Feb 7 at 3:01
Nikhil ChilwantNikhil Chilwant
1285
1285
add a comment |
add a comment |
Thanks for contributing an answer to Mathematics Stack Exchange!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function () {
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f31725%2fintuition-behind-matrix-multiplication%23new-answer', 'question_page');
}
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function () {
StackExchange.helpers.onClickDraftSave('#login-link');
});
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
67
$begingroup$
Do you think of $3.9289482948290348290 times 9.2398492482903482390$ as repetitive addition?
$endgroup$
– lhf
Apr 8 '11 at 12:43
13
$begingroup$
It depends on what you mean by 'meaning'.
$endgroup$
– Mitch
Apr 8 '11 at 12:58
17
$begingroup$
I believe a more interesting question is why matrix multiplication is defined the way it is.
$endgroup$
– M.B.
Apr 8 '11 at 13:01
5
$begingroup$
I can't help but read your question's title in Double-Rainbow-man's voice...
$endgroup$
– Adrian Petrescu
Apr 8 '11 at 16:04
4
$begingroup$
You probably want to read this answer of Arturo Magidin's: Matrix Multiplication: Interpreting and Understanding the Multiplication Process
$endgroup$
– Uticensis
Apr 8 '11 at 16:42