Vrftsjtryk

Projektion eines Tesseraktes (vierdimensionaler Hyperwürfel) in die 2. Dimension

Hyperwürfel oder Maßpolytope sind n{displaystyle n}-dimensionale Analogien zum Quadrat (n=2{displaystyle n=2}) und zum Würfel (n=3{displaystyle n=3}). Dabei kann n{displaystyle n} eine beliebige natürliche Zahl sein. Der vierdimensionale Hyperwürfel wird auch als Tesserakt bezeichnet. Die Symmetriegruppe eines Hyperwürfels ist die Hyperoktaedergruppe.

Konstruktion regulärer Würfel |

Reguläre Würfel der Kantenlänge a≠0{displaystyle aneq 0} lassen sich wie folgt erzeugen:

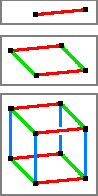
• Wenn ein Punkt um die Distanz a{displaystyle a} geradlinig verschoben wird, entsteht eine eindimensionale Strecke, mathematisch ein eindimensionaler Hyperwürfel.


• Wenn diese Strecke senkrecht zu ihrer Dimension um die Distanz a{displaystyle a} verschoben wird, entsteht ein zweidimensionales Quadrat, eine Fläche, mathematisch ein zweidimensionaler Hyperwürfel.


• Wenn dieses Quadrat senkrecht zu seinen beiden Dimensionen um die Distanz a{displaystyle a} verschoben wird, entsteht ein dreidimensionaler Würfel, mathematisch einem dreidimensionalen Hyperwürfel entsprechend.


• Allgemein: Wenn also ein n{displaystyle n}-dimensionaler Würfel senkrecht zu seinen n{displaystyle n} Dimensionen um die Distanz a{displaystyle a} verschoben wird, entsteht ein (n+1){displaystyle (n+1)}-dimensionaler Hyperwürfel.

Grenzelemente |

In einem Hyperwürfel der Dimension n{displaystyle n} befinden sich an jedem Knoten (Ecke) genau n{displaystyle n} Kanten. Demnach handelt es sich bei einem Hyperwürfel um einen ungerichteten Multigraph (siehe auch: Graphentheorie).

Der n{displaystyle n}-dimensionale Würfel wird von nulldimensionalen, eindimensionalen, …, (n−1){displaystyle (n!-!1)}-dimensionalen Elementen begrenzt.
Am Beispiel:

Der 3-dimensionale Würfel wird von Knoten (Punkten), Kanten (Strecken) und Flächen begrenzt, also von Elementen der Dimension 0,1 und 2.

Die Anzahl der einzelnen Grenzelemente lässt sich aus folgender Überlegung ableiten:
Sei ein Hyperwürfel von der Dimension n+1{displaystyle n!+!1} gegeben. Die k{displaystyle k}-dimensionalen Grenzelemente dieses Würfels (kn+1{displaystyle k_{n+1}}) lassen sich folgendermaßen aus den Grenzelementen eines n{displaystyle n}-dimensionalen Hyperwürfels erzeugen: Die k{displaystyle k}-dimensionalen Grenzelemente (kn{displaystyle k_{n}}) verdoppeln sich und alle k−1{displaystyle k!-!1} dimensionalen Elemente (k−1)n{displaystyle (k!-!1)_{n}} werden zu k{displaystyle k}-dimensionalen erweitert. Somit ergibt sich in der Summe eine Anzahl von kn+1=2kn+(k−1)n{displaystyle k_{n+1}=2k_{n}+(k-1)_{n}}.

Beispiel

• Der 2-dimensionale Hyperwürfel wird von 1 Fläche (kn=2){displaystyle (k_{n}=2)}, 4 Kanten (kn=1){displaystyle (k_{n}=1)} und 4 Knoten (kn=0){displaystyle (k_{n}=0)} begrenzt.

• Der 3-dimensionale Würfel wird von 2+4=6{displaystyle 2+4=6} Flächen (kn+1=2){displaystyle (k_{n+1}=2)} begrenzt, von 8+4=12{displaystyle 8+4=12} Kanten (kn+1=1){displaystyle (k_{n+1}=1)} und 4+4=8{displaystyle 4+4=8} Knoten (kn+1=0){displaystyle (k_{n+1}=0)}.

Anders kann man sich überlegen: Wenn man einen n{displaystyle n}-dimensionalen Hyperwürfel in ein kartesisches Koordinatensystem um den Ursprung zentriert und nach den Koordinatenachsen ausgerichtet legt, gibt es zu einem k{displaystyle k}-dimensionalen Grenzelement k{displaystyle k} Koordinatenachsen, die parallel zu diesem Grenzelement sind. Andererseits gibt es aber zu jeder Auswahl von k{displaystyle k} Koordinatenachsen nicht nur ein k{displaystyle k}-dimensionales Grenzelement, sondern 2n−k,{displaystyle 2^{n-k},} weil man durch jede der n−k{displaystyle n-k} zu den Grenzelementen senkrechten Achsen die Anzahl der Grenzelemente verdoppelt (es gibt dieselben Grenzelemente noch einmal parallelverschoben auf der anderen Seite der Achse). Die Anzahl der Grenzelemente ergibt sich also aus dem Produkt der Anzahl der Möglichkeiten, k{displaystyle k} Achsen aus den n{displaystyle n} Achsen auszuwählen, mit der Anzahl von Grenzelementen für jede Auswahl und lautet somit (nk)⋅2n−k{displaystyle {binom {n}{k}}cdot 2^{n-k}} (mit dem Binomialkoeffizienten (nk){displaystyle {binom {n}{k}}}).

Der Weg zum Hyperwürfel

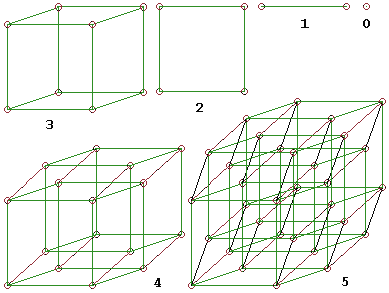
Die 0- bis 5-dimensionalen Würfel in der Parallelprojektion

	Schläfli- Symbol	Anzahl der Grenzelemente
		0-dim.	1-dim.	2-dim.	3-dim.	4-dim.	…{displaystyle ldots }	(n−1){displaystyle (n!-!1)}-dim.	n{displaystyle n}-dim.
Punkt	(){displaystyle ()}	1
Strecke	{}{displaystyle {}}	2	1
Quadrat	{4}{displaystyle {4}}	4	4	1
3-dim. Würfel	{4,3}{displaystyle {4,3}}	8	12	6	1
4-dim. Würfel	{4,3,3}{displaystyle {4,3,3}}	16	32	24	8	1
⋮{displaystyle vdots }
n{displaystyle n}-dim. Würfel	{4,3n−2}{displaystyle {4,3^{n-2}}}	2n{displaystyle 2^{n}}	n2n−1{displaystyle n2^{n-1}}	(n2)2n−2{displaystyle {binom {n}{2}}2^{n-2}}	(n3)2n−3{displaystyle {binom {n}{3}}2^{n-3}}	…{displaystyle ldots }	…{displaystyle ldots }	(nn−1)21=2n{displaystyle {binom {n}{n-1}}2^{1}=2n}	(nn)20=1{displaystyle {binom {n}{n}}2^{0}=1}

Jedes k{displaystyle k}-dimensionale Grenzelement eines n{displaystyle n}-dimensionalen Würfels der Kantenlänge a{displaystyle a} ist für 0<k≤n{displaystyle 0<kleq n} ein k{displaystyle k}-dimensionaler Würfel derselben Kantenlänge a{displaystyle a}. Damit hat ein 4-Hyperwürfel 16 Ecken, ein Kantennetz der Länge 32a{displaystyle 32a}, ist begrenzt von einem Flächennetz der Gesamtfläche 24a2{displaystyle 24a^{2}} und von Zellen mit dem 3-Gesamtvolumen (der 3-dimensionalen Hyperfläche) von 8a3{displaystyle 8a^{3}} und hat ein 4-Volumen von a4{displaystyle a^{4}}.

Eigenschaften |

Die Konstruktion der längsten Diagonalen von Quadrat, Würfel und Tesserakt

Der Name Maßpolytop kommt von der Möglichkeit, das Objekt parallel zu allen Koordinatenachsen auszurichten und den euklidischen Raum durch parallele Vervielfältigung restlos auszufüllen. Es ist das einzige regelmäßige Polytop, mit dem dies in Dimensionen n>4{displaystyle n>4} gelingt. Für jede Dimension sind diese Parkettierungen selbstdual mit dem Schläfli-Symbol {4,3n−2,4}.{displaystyle {4,3^{n-2},4}.}

Die längste Diagonale eines Hyperwürfels entspricht der Quadratwurzel seiner Dimension multipliziert mit seiner Kantenlänge.

Maßpolytop (oder Hyperwürfel) und Kreuzpolytop (oder Hyperoktaeder) sind zueinander dual. Daher stimmen auch ihre Symmetriegruppen überein.

Dimension	Kanten	Knoten	Seiten	Grad	Durchmesser	Kanten-Zusammenhang	Knoten-Zusammenhang
1	1{displaystyle 1}	2{displaystyle 2}	2{displaystyle 2}	1{displaystyle 1}	1{displaystyle 1}	1{displaystyle 1}	1{displaystyle 1}
2	4{displaystyle 4}	4{displaystyle 4}	4{displaystyle 4}	2{displaystyle 2}	2{displaystyle 2}	2{displaystyle 2}	2{displaystyle 2}
3	12{displaystyle 12}	8{displaystyle 8}	6{displaystyle 6}	3{displaystyle 3}	3{displaystyle 3}	3{displaystyle 3}	3{displaystyle 3}
4	32{displaystyle 32}	16{displaystyle 16}	8{displaystyle 8}	4{displaystyle 4}	4{displaystyle 4}	4{displaystyle 4}	4{displaystyle 4}
...	...	...	...	...	...	...	...
n{displaystyle n}	2(n−1)⋅n{displaystyle 2^{(n-1)}cdot n}	2n{displaystyle 2^{n}}	2n{displaystyle 2n}	n{displaystyle n}	n{displaystyle n}	n{displaystyle n}	n{displaystyle n}

Kunstanwendungen |

Bildende Kunst |

In der Bildenden Kunst beschäftigen sich viele Künstler mit dem Hyperwürfel.

• 
  Tony Robbin – durch Spiegelungen und Verdrehungen von Würfel- Kanten erzeugt Tony Robbin in Zeichnungen und mit Raum-Installationen Situationen, die nur in einer hyperdimensionalen Welt möglich wären.


• 
  Manfred Mohr – veranschaulicht in seinen Kompositionen Interaktionen von Linien, die einer räumlichen Logik von mehr als drei Freiheitsgraden folgen.


• 
  Frank Richter – konkretisiert in Grafiken, Plastiken und Rauminstallationen nach der Vorgabe von mathematischen Regeln Raum-Konstellationen, die über die dritte Dimension hinausgehen.


• 
  Salvador Dalí hat in seinem Bild Kreuzigung (Corpus Hypercubus) 1954 einen gekreuzigten Jesus auf das Netz eines Hyperwürfels gemalt.^[2]
  

Projektion eines rotierenden Hyperwürfels

Hyperwürfel in der Popkultur |

• Der Film Cube 2: Hypercube handelt von einem Hyperwürfel, in dem sich die Charaktere in den drei räumlichen Dimensionen und einer zeitlichen Dimension bewegen und sich beispielsweise selbst in einem anderen Zeitabschnitt begegnen.


• Die Kurzgeschichte And He Built a Crooked House, in der deutschen Version Das 4D-Haus, von Robert A. Heinlein behandelt ein Haus, das aus einem Hyperwürfel besteht.


• Die Progressive-Metal-Band Tesseract^[3] hat sich nach dem 4D Hyperkubus (engl. tesseract; Tesserakt) benannt und verwendet verschiedene Projektionen und Animationen davon als Bandlogo.


• Der Roman Apocalypsis III des Autors Mario Giordano verwendet einen Tesserakt als Gestalt der Büchse der Pandora
  

Siehe auch |

• Euklidischer Raum


• 
  Hilbertwürfel für den unendlichdimensionalen Fall


• 
  Hyperrechteck (alias Hyperquader) – Verallgemeinerung für unterschiedliche Kantenlängen


• Hyperebene


• Hyperpyramide


• Hyperraum

Weblinks |

• 
  Der n-dimensionale Hyperwürfel (PDF; 3,5 MB)


• Hyperwürfel und Hyperkugeln


• Erweiterte Grenzelemente-Tabelle


• 
  Animierter Hyperwürfel (Java)


• 
  4d-screen.de – vier-, fünf-, sechs- und siebendimensionale Würfel (Java)


• Bebilderte Konstruktion eines 4D-Hyperwürfels

Einzelnachweise |

1. 
   ↑ Die Bewegungen eines Punktes innerhalb eines Hyperwürfels: schieben auf einer geraden Linie; drehen als Bewegung auf einer gekrümmten Bahn in einer Ebene; winden als Bewegung auf einer gekrümmten Bahn in drei Dimensionen; stülpen als Bewegung auf einer vierdimensional gekrümmten Bahn.
   


2. 
   ↑ Beispiel eines Dalígemäldes (Memento des Originals vom 23. Juli 2015 im Internet Archive)  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.poster.net
   


3. 
   ↑ Tesseract