Vrftsjtryk

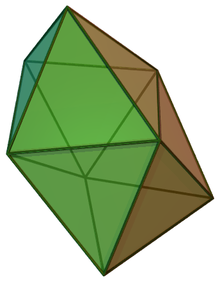
Das Trigondodekaeder, ein Polyeder, das nur von regelmäßigen Dreiecken begrenzt ist.

Ein (dreidimensionales) Polyeder [.mw-parser-output .IPA a{text-decoration:none}poliˈʔeːdɐ] (auch Vielflach, Vielflächner oder Ebenflächner; von griechisch πολύς .mw-parser-output .Latn{font-family:"Akzidenz Grotesk","Arial","Avant Garde Gothic","Calibri","Futura","Geneva","Gill Sans","Helvetica","Lucida Grande","Lucida Sans Unicode","Lucida Grande","Stone Sans","Tahoma","Trebuchet","Univers","Verdana"}polýs, „viel“, und ἕδρα hedra, „Sitz(fläche)“) ist im engeren Sinne eine Teilmenge des dreidimensionalen Raumes, welche ausschließlich von geraden Flächen (Ebenen) begrenzt wird, beispielsweise ein Würfel oder ein Oktant eines dreidimensionalen Koordinatensystems.

Beispiele für Polyeder |

Die meisten Spielwürfel sind polyederförmig.

Kuppelgewächshaus im Botanischen Garten Düsseldorf

Beispiele für Polyeder aus dem Alltag – verstanden als geometrische Körper – sind (in ihrer üblichen Bauweise) Schränke, Pyramiden, Häuser, Kristalle, Spielwürfel oder Geodätische Kuppeln. Keine Polyeder sind hingegen Kugeln, Kegel, Flaschen, Tortenstücke, da sie gekrümmte Randflächen besitzen. Die wichtigsten Polyeder sind Würfel, Quader, Prismen, Pyramiden und Spate (Parallelepipede).

Besondere dreidimensionale Polyeder |

Polyeder, wie sie uns im Alltag begegnen bzw. wie man sie von der Schulmathematik her kennt (vgl. vorhergehender Abschnitt), sind dreidimensional und beschränkt, also – im Sinne der Topologie – kompakte Teilmengen des dreidimensionalen euklidischen Raums. Sie zählen damit zu den geometrischen Körpern. Ein Polyeder heißt dabei dreidimensional, wenn er in keiner Ebene vollständig enthalten ist. Ein Polyeder heißt beschränkt, wenn es eine Kugel gibt, in der das Polyeder vollständig enthalten ist. Unbeschränkte Polyeder mit nur einer Ecke werden Polyederkegel genannt. Dazu zählen etwa die Trieder (englisch trihedron).

Konvexe Polyeder |

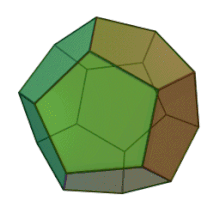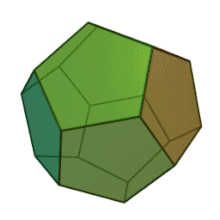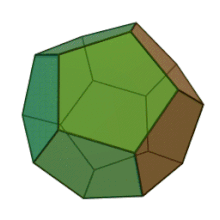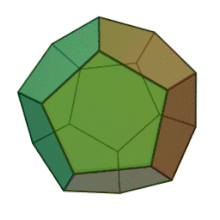
Das Dodekaeder, ein platonischer Körper.

Häufig sind dreidimensionale Polyeder zudem konvex. Ein Polyeder heißt konvex, wenn für je zwei Punkte des Polyeders die Verbindungsstrecke zwischen diesen Punkten vollständig im Polyeder liegt. Zum Beispiel ist das nebenstehende Dodekaeder konvex. Ein Beispiel eines nicht-konvexen Polyeders ist das unten gezeigte toroidale Polyeder.

Reguläre Polyeder |

Bei Polyedern können verschiedene Arten von Regelmäßigkeiten auftreten. Die wichtigsten sind:

1. Die Seitenflächen sind regelmäßige Vielecke.


2. Alle Seitenflächen sind kongruent.


3. Alle Ecken sind gleichartig, das heißt, für je zwei Ecken P,Q{displaystyle P,Q} kann man das Polyeder so drehen oder spiegeln, dass P{displaystyle P} in Q{displaystyle Q} überführt wird und das neue Polyeder mit dem ursprünglichen zur Deckung kommt.

Polyeder, die alle 3 Bedingungen erfüllen, heißen reguläre Polyeder.

Platonische, Archimedische, Catalanische und Johnson-Körper |

Es gibt genau 5 konvexe Polyeder, die reguläre Polyeder sind (also alle drei Bedingungen erfüllen), die platonischen Körper.

Die konvexen Polyeder, die nur die erste und die dritte Bedingung erfüllen, sind (gewisse) Prismen, Antiprismen sowie die 13 archimedischen Körper.

Die konvexen Polyeder, die nur die zweite Bedingung erfüllen, sind die 13 catalanischen Körper. Genauer gesagt muss für diese die etwas stärkere Bedingung der Gleichartigkeit der Seiten (analog zu 3.) erfüllt sein.

Die konvexen Polyeder, die nur die erste Bedingung erfüllen, sind die 92 Johnson-Körper.

Orthogonale Polyeder |

Die Flächen eines orthogonalen Polyeders treffen sich im rechten Winkel. Seine Kanten verlaufen parallel zu den Achsen eines kartesischen Koordinatensystems. Mit Ausnahme des Quaders sind orthogonale Polyeder nicht konvex. Sie erweitern die zweidimensionalen orthogonalen Polygone in die dritte Dimension. Orthogonale Polyeder kommen in der algorithmischen Geometrie zum Einsatz. Dort bietet ihre eingeschränkte Struktur Vorteile beim Bewältigen ansonsten ungelöster Probleme (beliebiger Polyeder). Ein Beispiel ist das Entfalten der Polyederflächen in ein polygonales Netz.

Chirale Polyeder |

Chirale Polyeder sind Vielflächner, die nicht mit ihrem Spiegelbild übereinstimmen. Beispiele in drei Dimensionen sind der abgeschrägte Würfel und das schiefe Dekaeder. Sie weisen Händigkeit auf, das heißt, sie besitzen eine rechtshändige und eine linkshändige Variante, die durch Spiegelung aufeinander abgebildet werden können.^[1]

Eulerscher Polyedersatz und Euler-Charakteristik |

Für konvexe und beschränkte Polyeder gilt der eulersche Polyedersatz:

E+F−K=2.{displaystyle E+F-K=2.}

Dabei ist E{displaystyle E} die Anzahl der Ecken, F{displaystyle F} die Anzahl der Flächen und K{displaystyle K} die Anzahl der Kanten.

Ein toroidales Polyeder, zusammengesetzt aus 48 gleichseitigen Dreiecken

Die Bedingung „konvex“ ist wesentlich. Beispiel: Die Punkte des dreidimensionalen Raumes mit den (rechtwinkligen kartesischen) Koordinaten (x,y,z), wobei der Absolutbetrag von x, y und z jeweils kleiner oder gleich 2 ist, bilden einen Würfel der Kantenlänge 4. Wenn wir aus ihm die Punkte entfernen, deren Koordinaten alle vom Betrag <1 sind, entsteht ein nichtkonvexer Polyeder, nämlich ein Würfel, aus dessen Innerem ein kleinerer Würfel ausgebohrt ist, mit 16 Ecken, 24 Kanten und 12 Flächen, in dem der eulersche Polyedersatz nicht gilt.

Für zusammenhängende Polyeder (zu denen das obige Beispiel nicht gehört) gilt allgemein

E+F−K=χ{displaystyle E+F-K=chi }

mit der Euler-Charakteristik χ{displaystyle chi }. Für einen Torus zum Beispiel ist χ=0{displaystyle chi =0}. Das rechts abgebildete Polyeder ist ein Beispiel dafür. Es hat 24 Ecken, 72 Kanten und 48 Flächen: E−K+F=24−72+48=0{displaystyle E-K+F=24-72+48=0}.

Benennung |

Polyeder werden allgemein nach der Anzahl der begrenzenden Flächen klassifiziert.

Flächenzahl	Name	Beispiel	Bild
4	Tetraeder	= Dreieckpyramide
5	Pentaeder	Quadratpyramide
6	Hexaeder	Würfel
7	Heptaeder	verlängerte Dreieckpyramide
8	Oktaeder	Rhomboederstumpf
9	Enneaeder	verlängerte Quadratpyramide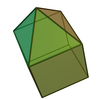
10	Dekaeder	Fünfeck-Bipyramide
11	Hendekaeder
12	Dodekaeder	regelmäßiges Dodekaeder
13	Tridekaeder	verdreht verlängerte Quadratpyramide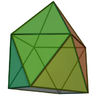
14	Tetradekaeder	Disheptaeder
15	Pentadekaeder	verlängerte Fünfecksbipyramide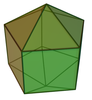
16	Hexadekaeder	zweifach erweitertes Antiprisma
17	Heptadekaeder	erweiterte Sphenocorona
18	Oktadekaeder	Quadratdoppelkuppel
19	Enneadekaeder
20	Ikosaeder	regelmäßiges Ikosaeder
22	Ikosidiploeder	verlängerte Fünfeckskuppel
24	Ikositetraeder	Deltoidalikositetraeder
30	Triacontaeder	doppelt erweitertes abgestumpftes Hexaeder
32	Triacontadiploeder	Ikosaederstumpf
60	Hexakontaeder	doppelt erweitertes abgestumpftes Hexaeder
		Pentagonhexakontaeder

Verallgemeinerungen |

Vielfach wird neben dem Begriff des Polytops auch der Begriff „Polyeder“ für nicht notwendigerweise dreidimensionale Räume verwendet.

• Vor allem in der Topologie nennt man eine Teilmenge des Rn{displaystyle mathbb {R} ^{n}} ein Polyeder, wenn sie triangulierbar ist, wenn sie also als Vereinigung der Simplexe eines simplizialen Komplexes K⊆2Rn{displaystyle {mathcal {K}}subseteq 2^{mathbb {R} ^{n}}} gebildet werden kann.^[2][3] Das homöomorphe Bild eines solchen allgemeinen Polyeders bezeichnet man als krummes Polyeder und die Bilder der beteiligten Simplexe als krumme Simplexe.^[4]
  


• In der linearen Optimierung ist ein (konvexes) Polyeder im Rn{displaystyle mathbb {R} ^{n}} definiert als der Schnitt von endlich vielen Halbräumen.^[5] Nach dieser Definition ist ein Polyeder nicht notwendigerweise beschränkt. Ein beschränktes nichtleeres Polyeder wird dann als Polytop bezeichnet. Nach dem Zerlegungssatz für konvexe Polyeder ist eine Teilmenge des Rn{displaystyle mathbb {R} ^{n}} genau dann ein Polyeder, wenn sie sich als Summe eines konvexen Polytops und eines (konvexen) polyedrischen Kegels darstellen lässt.

Weblinks |

 Commons: Polyeder – Album mit Bildern, Videos und Audiodateien

 Wiktionary: Polyeder – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• 
  Polyedergarten Bilder, Animationen, VRML-3D-Modelle; mit ästhetischem Anspruch


• Formeln für reguläre und semireguläre Polyeder


• 
  Paper Models of Polyhedra Schablonen zum Basteln von Polyedern


• 
  Polyeder aus Flechtstreifen Polyedermodelle durch Verflechten von Papierstreifen ohne Klebstoff herstellen

Einzelnachweise |

1. 
   ↑ Edward S. Popko: Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press, 2012, ISBN 978-1-4665-0429-5 (eingeschränkte Vorschau in der Google-Buchsuche). 
   


2. 
   ↑ Egbert Harzheim: Einführung in die Kombinatorische Topologie (= DIE MATHEMATIK. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X, S. 34 (MR0533264). 
   


3. 
   ↑ John M. Lee: Introduction to Topological Manifolds (Graduate Texts in Mathematics 202). Springer, New York [u. a.] 2000, ISBN 0-387-98759-2, S. 149. 
   


4. 
   ↑ Egbert Harzheim: Einführung in die Kombinatorische Topologie (= DIE MATHEMATIK. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X, S. 35 (MR0533264). 
   


5. 
   ↑ Rainer E. Burkhard, Uwe T. Zimmermann: Einführung in die Mathematische Optimierung (= Springer-Lehrbuch). Springer, Berlin/Heidelberg 2013, ISBN 978-3-642-28673-5, S. 19.