Prisma (Geometrie)
Ein Prisma mit einem Sechseck als Grundfläche
Ein Prisma (Mehrzahl: Prismen) ist ein geometrischer Körper, der durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht (man spricht auch von einer Extrusion des Vielecks). Ein Prisma ist damit ein spezielles Polyeder.
Das gegebene Vieleck wird als Grundfläche bezeichnet, die gegenüberliegende Seite (oder Begrenzungsfläche) als Deckfläche. Die Gesamtheit aller übrigen Begrenzungsflächen heißt Mantelfläche. Die Seitenkanten des Prismas, die Grund- und Deckfläche verbinden, sind zueinander parallel und alle gleich lang. Grund- und Deckfläche sind zueinander kongruent (deckungsgleich) und parallel.
Inhaltsverzeichnis
1 Gerades und schiefes Prisma
2 Sonderfälle und Verallgemeinerung
3 Formeln für Volumen, Mantel- und Oberfläche
4 Siehe auch
5 Literatur
6 Weblinks
Gerades und schiefes Prisma |
A: gerades Prisma; B: schiefes Prisma
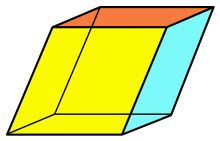
Spezialfall eines schiefen Prismas: Parallelepiped, hier sogar ein Rhomboeder
Erfolgt die Parallelverschiebung des Vielecks senkrecht zur Grundfläche, spricht man von einem geraden Prisma, ansonsten von einem schiefen Prisma. Die Mantelfläche eines geraden Prismas besteht aus Rechtecken, im allgemeinen Fall besteht sie aus Parallelogrammen.
Der zu einem geraden Prisma duale Körper ist eine Doppelpyramide (auch: Bipyramide).
Sonderfälle und Verallgemeinerung |
Eine besondere Form des Prismas ist der Quader. Beim Quader kann jede Seite als Grundfläche des Prismas aufgefasst werden.
In der Optik versteht man unter einem Prisma meistens ein gerades Prisma mit einem Dreieck als Grundfläche, siehe Prisma (Optik).
Das Prisma ist in der Mathematik ein Spezialfall des allgemeinen Zylinders.
Formeln für Volumen, Mantel- und Oberfläche |
Das Volumen V{displaystyle V}
V=G⋅h{displaystyle V=Gcdot h},
wobei G{displaystyle G}
Aus dem Prinzip von Cavalieri folgt, dass zwei Prismen (etwa ein gerades und ein schiefes Prisma) bei gleicher Grundfläche und Höhe das gleiche Volumen besitzen.
Die Mantelfläche M{displaystyle M}
M=U⋅h{displaystyle M=Ucdot h},
wobei U{displaystyle U}
Die gesamte Oberfläche O{displaystyle O}
O=2⋅G+M{displaystyle O=2cdot G+M},
wobei G{displaystyle G}
Siehe auch |
- Antiprisma
Literatur |
Prisma. In: Meyers Großes Konversations-Lexikon, Band 16. Leipzig 1908, S. 354.
Weblinks |
Commons: Prismen – Sammlung von Bildern, Videos und Audiodateien
Wiktionary: Prisma – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
Prisma auf mathematische-basteleien.de
Eric W. Weisstein: Prism. In: MathWorld (englisch).
