Vrftsjtryk

 Nota: Para outros significados, veja Triângulo (desambiguação).

Triângulo ou trilátero.
Um triângulo
Tipo	polígono convexo
Arestas e Vértices	3
Símbolo de Schläfli	{3} (se for equilátero)
Área	vários métodos; ver abaixo
Ângulo interno (graus)	60° (se for equilátero)

No plano, o triângulo (também aceito como trilátero^[1]) é a figura geométrica que ocupa o espaço interno limitado por três segmentos de reta que concorrem, dois a dois, em três pontos diferentes formando três lados e três ângulos internos que somam 180°.^[2] Também se pode definir um triângulo em superfícies gerais. Nesse caso, são chamados de triângulos geodésicos e têm propriedades diferentes. Também podemos dizer que o triângulo é a união de três pontos não-colineares (pertencente a um plano, em decorrência da definição dos mesmos), por três segmentos de reta.^[3]

O triângulo é o único polígono que não possui diagonais e cada um de seus ângulos externos é suplementar do ângulo interno adjacente.^[3] O perímetro de um triângulo é a soma das medidas dos seus lados. Denomina-se a região interna de um triângulo de região convexa (curvado na face externa) e a região externa de região côncava (curvado na face interna).

Definição |

Os ângulos A^,{displaystyle {hat {A}},} B^{displaystyle {hat {B}}} e C^{displaystyle {hat {C}}} são ângulos internos de DE^A,{displaystyle D{hat {E}}A,} enquanto E^{displaystyle {hat {E}}} é ângulo externo.

Na geometria euclidiana plana, definimos um triângulo da seguinte forma:

Dados três pontos, A,{displaystyle A,} B{displaystyle B} e C,{displaystyle C,} não colineares, à reunião dos segmentos AB¯,{displaystyle {overline {AB}},} AC¯{displaystyle {overline {AC}}} e BC¯{displaystyle {overline {BC}}} chama-se triângulo ABC,{displaystyle ABC,} denotado por △ABC.{displaystyle triangle {ABC}.}

Assim:

△A,B,C=A,B¯∪A,C¯∪B,C¯{displaystyle triangle {A,B,C}={overline {A,B}}cup {overline {A,C}}cup {overline {B,C}}}^[4]

Elementos de um Triângulo |

• 
  Vértices: os pontos A,{displaystyle A,} B{displaystyle B} e C{displaystyle C} são os vértices do △ABC.{displaystyle triangle {ABC}.}
  


• 
  Lados: os segmentos AB¯{displaystyle {overline {AB}}} (de medida c), AC¯{displaystyle {overline {AC}}} (de medida b) e BC¯{displaystyle {overline {BC}}} (de medida a), são os lados do triângulo ABC.{displaystyle ABC.}
  


• 
  Ângulos internos: os ângulos BA^C{displaystyle B{hat {A}}C} ou A^,{displaystyle {hat {A}},} AB^C{displaystyle A{hat {B}}C} ou B^{displaystyle {hat {B}}} e AC^B{displaystyle A{hat {C}}B} ou C^{displaystyle {hat {C}}} são os ângulos internos do triângulo ABC,{displaystyle ABC,} ou seja, são os ângulos entre os lados de um triângulo.


• 
  Ângulos externos: são os ângulos formados pelo prolongamento de um dos lados com um lado adjacente. Por exemplo, se tomarmos a semirreta BC→{displaystyle {overrightarrow {BC}}} e um ponto D{displaystyle D} sob ela, mas externo ao triângulo, e o lado AC¯,{displaystyle {overline {AC}},} temos o ângulo AC^D,{displaystyle A{hat {C}}D,} que é um ângulo externo do triângulo ABC.{displaystyle ABC.}
  

Diz-se que os lados AB¯,{displaystyle {overline {AB}},} AC¯,{displaystyle {overline {AC}},} BC¯{displaystyle {overline {BC}}} e os ângulos C^,{displaystyle {hat {C}},} B^{displaystyle {hat {B}}} e A^{displaystyle {hat {A}}} são, respectivamente, opostos.^[4]

Os Tipos de Triângulos |

Os triângulos podem ser classificados conforme as relações entre seus lados ou entre seus ângulos.^[2]

Quanto aos lados |

Quanto aos lados temos três tipos de triângulos: equiláteros, isósceles e escalenos.

Triângulo Equilátero |

Ver artigo principal: Triângulo equilátero

Um triângulo é equilátero se, e somente se, têm os três lados congruentes.

Isso significa que um triângulo equilátero é um triângulo que possui todos os lados congruentes, ou seja, iguais. Um triângulo equilátero é também equiângulo: todos os seus ângulos internos são congruentes (medem 60°),^[3] sendo, portanto, classificado como um polígono regular.

Triângulos Isósceles |

Ver artigo principal: Triângulo isósceles

Um triângulo é isósceles se, e somente se, pelo menos dois de seus três lados forem congruentes.

Isso significa que um triângulo isósceles possui pelo menos dois lados de mesma medida. Assim temos que todo triângulo equilátero é, consequentemente, um caso especial de triângulo isósceles, que apresenta não somente dois, mas todos os lados congruentes. Num triângulo isósceles, o ângulo formado pelos lados congruentes é chamado ângulo do vértice. Os demais ângulos denominam-se ângulos da base e são congruentes.

Em todo triângulo isósceles os ângulos opostos aos lados congruentes são congruentes.^[5]

Triângulo Escaleno |

Um triângulo é escaleno se, e somente se, dois quaisquer lados não são congruentes.

Isso significa que em um triângulo escaleno as medidas dos três lados são diferentes. Assim, os ângulos internos de um triângulo escaleno também possuem medidas diferentes.

• 
  

  

  
  

  
  

  Triângulo equilátero
  

  
  

  
  


• 
  

  

  
  

  
  

  Triângulo isósceles
  

  
  

  
  


• 
  

  

  
  

  
  

  Triângulo escaleno
  

  
  

  
  

Quanto aos ângulos |

Quanto aos ângulos, podemos ter três tipos de triângulo: retângulo, obtusângulo e acutângulo.

• Um triângulo retângulo possui um ângulo reto.^[2] Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados chamam-se catetos. Os ângulos agudos de um triângulo retângulo, opostos aos catetos, são complementares (ou seja, sua soma é igual a 90°).


• Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos.


• Em um triângulo acutângulo, os três ângulos são agudos.

• 
  

  

  
  

  
  

  Triângulo retângulo
  

  
  

  
  


• 
  

  

  
  

  
  

  Triângulo obtusângulo
  

  
  

  
  


• 
  

  

  
  

  
  

  Triângulo acutângulo
  

  
  

  
  

Condição de existência de um triângulo |

Para que se possa construir um triângulo é necessário que a medida de qualquer um dos lados seja menor que a soma das medidas dos outros dois e maior que o valor absoluto da diferença entre essas medidas.

|b−c|<a<b+c{displaystyle |b-c|<a<b+c}

Fatos básicos |

Fatos elementares sobre triângulos foram apresentados por Euclides nos livros 1-4 de sua obra Elementos aproximadamente em 300 a.C.

Um triângulo é um polígono.

Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais, e isso ocorre, por exemplo, quando dois triângulos compartilham um ângulo e os lados opostos a esse ângulo são paralelos entre si. O fato crucial sobre triângulos similares é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes o maior lado do triângulo similar, diz-se, então, que o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo.^[3] Assim, a razão do maior lado e o menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.

Usando-se triângulos retângulos e o conceito de similaridade, as funções trigonométricas de seno e cosseno podem ser definidas. Essas são funções de um ângulo que são investigadas na trigonometria.

Nos casos a seguir, será usado um triângulo com vértices A, B e C, ângulos α, β e γ e lados a, b e c. O lado a é oposto ao vértice A e ao ângulo α, o lado b é oposto ao vértice B e ao ângulo β e o lado c é oposto ao vértice C e ao ângulo γ.

Na Geometria euclidiana, de acordo com o Teorema angular de Tales, a 32ª proposição de Euclides afirma que a soma dos ângulos internos de qualquer triângulo é igual a dois ângulos retos (180° ou π radianos). Isso permite a determinação da medida do terceiro ângulo, desde que sejam conhecidas as medidas dos outros dois ângulos. Por exemplo:^[2]

α+β+γ=180∘{displaystyle alpha +beta +gamma =180^{circ }}

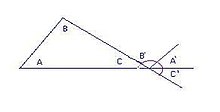
Os ângulos A e A' são iguais (duas paralelas cortadas por uma transversal). Os ângulos B e B' são iguais por serem alternos internos. Os ângulos C e C' são iguais por serem opostos pelo vértice. Assim vê-se que a soma dos ângulos internos do triângulo é 180º.

Existe um Corolário desse Teorema, que afirma que a medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não-adjacentes.

Ex: Sendo e{displaystyle e} a medida do ângulo externo do triângulo que tem como vértice o vértice C,{displaystyle C,} pode-se afirmar que: e=α+β{displaystyle e=alpha +beta }

Teorema de Pitágoras.

Um teorema central é o Teorema de Pitágoras, que afirma que em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos. Se o vértice C do exemplo dado for um ângulo reto, pode-se escrever isso da seguinte maneira:

c2=a2+b2{displaystyle c^{2}=a^{2}+b^{2}}

Isso significa que, conhecendo as medidas de dois lados de um triângulo retângulo, pode-se calcular a medida do terceiro lado — propriedade única dos triângulos retângulos.

O Teorema de Pitágoras pode ser generalizado pela lei dos cossenos:

c2=a2+b2−2⋅a⋅b⋅cos⁡γ{displaystyle c^{2}=a^{2}+b^{2}-2cdot acdot bcdot cos gamma }

Essa lei é válida para todos os triângulos, mesmo se γ não for um ângulo reto e pode ser usada para determinar o tamanho de lados e ângulos de um triângulo, desde que a medida de três ou dois lados e de um ângulo interno sejam conhecidas.

A lei dos senos diz:

senαa=senβb=senγc=1d{displaystyle {frac {mathrm {sen} ,alpha }{a}}={frac {mathrm {sen} ,beta }{b}}={frac {mathrm {sen} ,gamma }{c}}={frac {1}{d}}}

Existem dois triângulos retângulos especiais que aparecem frequentemente em geometria. O chamado "triângulo 45º-45º-90º" possui ângulos com essas medidas e a proporção de seus lados é: 1:1:2.{displaystyle 1:1:{sqrt {2}}.} O "triângulo 30º-60º-90º" possui ângulos com essas medidas e a proporção de seus lados é: 1:3:2.{displaystyle 1:{sqrt {3}}:2.}

Subdivisão de um triângulo |

É possível dividir um triângulo^[6] em outros menores internos de modo que em cada vértice incida o mesmo número de segmentos.
Sendo t a quantidade de triângulos e v o número de vértices.
Em cada vértice incide uma quantidade y de segmentos.
180t{displaystyle 180t} é a soma dos ângulos internos; 360(v−3){displaystyle 360(v-3)} é a soma dos ângulos em cada vértice no interior do triângulo.
A soma dos ângulos internos do triângulo é 180 graus. Então

180t=360(v−3)+180{displaystyle 180t=360(v-3)+180}

v=t+52{displaystyle v={frac {t+5}{2}}}

vy2{displaystyle {frac {vy}{2}}}

3t+32{displaystyle {frac {3t+3}{2}}}

vy2=3t+32{displaystyle {frac {vy}{2}}={frac {3t+3}{2}}}

y=3t+3v=3t+3(t+5)/2=6−24t+5.{displaystyle y={frac {3t+3}{v}}={frac {3t+3}{(t+5)/2}}=6-{frac {24}{t+5}}.}

t{displaystyle t}

t+5{displaystyle t+5}

t{displaystyle t}

y{displaystyle y}

v.{displaystyle v.}

As quatro possibilidades de divisão do triângulo.

Área |

Produto Base Altura

A área de um triângulo é a metade do produto da medida da sua altura pela medida da sua base. Assim, a área do triângulo pode ser calculada pela fórmula:

A=(B⋅h)2,{displaystyle A={(Bcdot h) over 2},}

Triângulos equiláteros

Se o triângulo for equilátero de lado l, sua área A pode ser obtida com:

A=l234.{displaystyle A={l^{2}{sqrt {3}} over 4}.}

Ou então usando sua altura h e a fórmula da base vezes a altura. A altura h de um triângulo equilátero é:

h=l32.{displaystyle h={l{sqrt {3}} over 2}.}

Vale notar que essas duas fórmulas para os triângulos equiláteros são obtidas usando as funções seno ou cosseno e usando a altura do triângulo, que o divide ao meio em dois triângulos retângulos iguais.

Semiperímetro

Ver artigo principal: Teorema de Heron

Outra maneira de calcular sua área é através do teorema de Herão (ou Heron), também conhecido como fórmula do semiperímetro:

A=s⋅(s−a)⋅(s−b)⋅(s−c),{displaystyle A={sqrt {scdot (s-a)cdot (s-b)cdot (s-c)}},}

onde:

s=(a+b+c)2{displaystyle s={(a+b+c) over 2}}

Lados

Também podemos calcular a área a partir dos lados do triângulo. Sendo a e b dois lados quaisquer de um triângulo, e α{displaystyle alpha } o ângulo entre eles, temos que a área é:

A=a⋅b⋅sen(α)2{displaystyle A={acdot bcdot sen(alpha ) over 2}}

Raio circunscrito

Ver artigo principal: Lei dos senos

Há ainda a fórmula da área do triângulo em função das medidas dos lados a,b,c{displaystyle a,b,c} e do raio da circunferência circunscrita a esse triângulo r,{displaystyle r,} demonstrada pela lei dos senos:

A=a⋅b⋅c4∗r{displaystyle A={acdot bcdot c over {4*r}}}

Pontos, linhas e círculos associados a um triângulo |

Mediatriz |

O circuncentro é o centro da circunferência circunscrita ao triângulo.

A mediatriz é a reta perpendicular a um lado do triângulo, traçada pelo seu ponto médio. As três mediatrizes de um triângulo se encontram em um único ponto, o circuncentro, que é o centro da circunferência circunscrita ao triângulo, que passa pelos três vértices do triângulo. O diâmetro dessa circunferência pode ser achado pela lei dos senos.

O teorema de Tales (ou Lei angular de Tales) determina que se o circuncentro estiver localizado em um lado do triângulo, o ângulo oposto a este lado será reto. Determina também que se o circuncentro estiver localizado dentro do triângulo, este será acutângulo; se o circuncentro estiver localizado fora do triângulo, este será obtusângulo.

Altura |

O ponto de interseção das alturas é o ortocentro.

Altura é um segmento de reta perpendicular a um lado do triângulo ou ao seu prolongamento, traçado pelo vértice oposto. Esse lado é chamado base da altura, e o ponto onde a altura encontra a base é chamado de pé da altura.

O ponto de interseção das três alturas de um triângulo denomina-se ortocentro (H). No triângulo acutângulo, o ortocentro é interno ao triângulo; no triângulo retângulo, é o vértice do ângulo reto; e no triângulo obtusângulo é externo ao triângulo. Os três vértices juntos com o ortocentro forma um sistema ortocêntrico.

A altura de todo e qualquer triângulo é dado pela fórmula:

h2=b2−(c−x)(c+x)⋅{displaystyle h^{2}={b^{2}-(c-x)(c+x)cdot }}

• b = hipotenusa do triângulo retângulo formado com a altura do triângulo em questão.


• h = altura procurada.


• c = base do triângulo.


• x = parte da base C do triângulo que foi dividida pela altura.

Mediana |

O ponto de interseção das três medianas é o baricentro ou centro de gravidade.

Mediana é o segmento de reta que une cada vértice do triângulo ao ponto médio do lado oposto. A mediana relativa à hipotenusa em um triângulo retângulo mede metade da hipotenusa.

O ponto de interseção das três medianas é o baricentro ou centro de gravidade do triângulo. O baricentro divide a mediana em dois segmentos.^[3] O segmento que une o vértice ao baricentro vale o dobro do segmento que une o baricentro ao lado oposto deste vértice. No triângulo equilátero, as medianas, mediatrizes, bissetrizes e alturas são coincidentes.^[2] No isósceles, apenas as que chegam ao lado diferente, no escaleno, nenhuma delas. Ainda para o triângulo Isósceles, vale ressaltar que a formação da bissetriz, coincidindo com o ponto médio de sua base, divide três semirretas iguais, as quais são percebidas com a inscrição do círculo formado pelo incentro da bissetriz, onde há duas semirretas, as quais serão o raios do círculo, sendo assim, dividindo-se em três partes iguais a altura do triângulo (que também coincide com a mediana e a bissetriz, cada 13{displaystyle {dfrac {1}{3}}}), explicam-se as relações de a semirreta que parte do ponto central do círculo até o lado do triângulo valer o mesmo que o raio, isto é, 13{displaystyle {dfrac {1}{3}}} e que o resto até o vértice oposto a esse lado valer 23.{displaystyle {dfrac {2}{3}}.}

Síntese para o triângulo isósceles, propriedade baricentro: semirretas divididas em dois segmentos, sendo que um é o dobro do outro. Entende-se portanto no triângulo isósceles que se uma parte vale 13,{displaystyle {dfrac {1}{3}},} a outra valerá o dobro: 2⋅13{displaystyle 2cdot {dfrac {1}{3}}} = 23.{displaystyle {dfrac {2}{3}}.}

Bissetriz |

O ponto de interseção das três bissetrizes é o incentro.

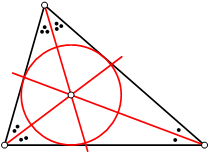
A bissetriz interna de um triângulo corresponde ao segmento de reta que parte de um vértice, e vai até o lado oposto do vértice em que partiu, dividindo o seu ângulo em dois ângulos congruentes.

Em um triângulo há três bissetrizes internas, sendo que o ponto de interseção delas chama-se incentro.

O círculo que tem o incentro como centro e é tangente aos três lados do triângulo é denominado círculo inscrito.

Já a bissetriz externa é o segmento da bissetriz de um ângulo externo situado entre o vértice e a interseção com o prolongamento do lado oposto.

As bissetrizes externas duas a duas têm um ponto de interseção, denominado ex-incentro relativo ao lado que contêm os vértices pelos quais passam essas retas.

Dado um ex-incentro, o círculo que tem esse ponto como centro, e é tangente a um lado e ao prolongamento dos dois outros lados do triângulo, é denominado círculo ex-inscrito.

Em um triângulo equilátero, o incentro, o ortocentro, o circuncentro e o baricentro são o mesmo ponto.

Reta de Euler |

Ver artigo principal: Reta de Euler

É a reta que contém o ortocentro, o baricentro e o circuncentro (os centros).

Círculo dos Nove Pontos |

É a circunferência que contém os pontos médios dos lados, os pés das alturas, e os pontos médios dos segmentos que unem o ortocentro aos vértices.

Relações de desigualdades entre lados e ângulos |

• 
  1ª relação: Um ângulo externo de um triângulo é o resultado da soma dos dois ângulos internos não-adjacentes.


• 
  2ª relação: Se dois lados de um triângulo têm medidas diferentes, ao maior lado opõe-se o maior ângulo e ao menor lado, opõe-se o menor ângulo.


• 
  3ª relação: Em todo triângulo, qualquer lado tem medida maior que a diferença entre as medidas dos outros dois.

Teorema da Base Média |

O teorema da base média do triângulo afirma que, dado um triângulo qualquer, o segmento com extremos nos pontos médios de dois lados desse triângulo é paralelo ao terceiro lado, e sua medida é igual a metade desse terceiro lado.^[4]

Demonstração |

Triângulo ABC qualquer.

Demonstração da base média

Dado um △ABC{textstyle triangle ABC} qualquer, sendo M ponto médio do lado AB¯{textstyle {overline {AB}}} e N o ponto médio do lado AC¯.{textstyle {overline {AC}}.} Queremos mostrar que MN¯//BC¯{textstyle {overline {MN}}/!/{overline {BC}}} e ainda MN=12BC.{textstyle MN={frac {1}{2}}BC.}

Hipótese: {AM¯≡MB¯AN¯≡NC¯{textstyle left{{begin{matrix}{overline {AM}}equiv {overline {MB}}\{overline {AN}}equiv {overline {NC}}end{matrix}}right.quad quad } Tese:{MN¯//BC¯MN=(12)BC{textstyle left{{begin{matrix}{overline {MN}}/!/{overline {BC}}\MN=left({frac {1}{2}}right)BCend{matrix}}right.}

Traçando s{displaystyle s} paralela a AB¯,{textstyle {overline {AB}},} passando por C. Onde MN↔∩s=D{textstyle {overleftrightarrow {MN}}cap s=D}

Pelo caso lado, ângulo, ângulo oposto: △AMN≡△CDN⇒{AN¯≡CN¯ (hipótese) AN^M≡CN^D (oposto pelo vértice) AM^N≡CD^N (alternos internos) {textstyle triangle AMNequiv triangle CDNRightarrow left{{begin{matrix}{overline {AN}}equiv {overline {CN}}{text{ (hipótese) }}\A{hat {N}}Mequiv C{hat {N}}D{text{ (oposto pelo vértice) }}\A{hat {M}}Nequiv C{hat {D}}N{text{ (alternos internos) }}end{matrix}}right.}

Consequentemente temos CD¯≡AM¯≡MB¯{displaystyle {overline {CD}}equiv {overline {AM}}equiv {overline {MB}}} e como CD¯//MB¯{displaystyle {overline {CD}}/!/{overline {MB}}} temos que BCDM é paralelogramo, logo MN¯//BC¯.{displaystyle {overline {MN}}/!/{overline {BC}}.} Ainda da congruência dos triângulos temos MN¯≡ND¯{displaystyle {overline {MN}}equiv {overline {ND}}} e como MD¯≡BC¯,{displaystyle {overline {MD}}equiv {overline {BC}},} então MN=12BC.{displaystyle MN={frac {1}{2}}BC.}

Ver também |

• Lista de construções do desenho geométrico

O wikilivro Matemática elementar tem uma página sobre Triângulos

• Trigonometria


• Triângulo de Pascal


• Triângulo de Sierpinski


• Triângulo de Penrose


• Triângulo de Ouro

Referências

Bibliografia |

• Boyer, Carl B. (1996). História da matemática. 2ª Edição. São Paulo. Edgard Blücher ltda. ISBN 85-212-0023-4.

Este artigo sobre geometria é um esboço. Você pode ajudar a Wikipédia expandindo-o. v d e

/math> ou