Vrftsjtryk

Parte de uma série sobre:
a constante matemática π{displaystyle {pi }}
Utilização
Área do círculo · Circunferência · Uso em outras fórmulas
Propriedades
Irracionalidade · Transcendência · Menor que 22/7
Valor
Aproximações · Memorização
Pessoas
Arquimedes · Liu Hui · Tsu Ch'ung Chih · Madhava de Sangamagrama · William Jones · John Machin · John Wrench · Ludolph van Ceulen · Ariabata
História
Cronologia · Livro
Na cultura
Legislação · Data
Tópicos relacionados
Quadratura do círculo · Problema de Basileia · Outros tópicos relacionados a π{displaystyle {pi }}
v d e

Na geometria euclidiana, uma circunferência é o lugar geométrico dos pontos de um plano que equidistam de um ponto fixo. O ponto fixo é o centro e a equidistância o raio da circunferência.^[1]

Definição Formal |

Circunferência é um conjunto dos pontos de um plano cuja distância a um ponto dado desse plano é igual a uma distância (não nula) dada. O ponto dado é o centro e a distância dada é o raio da circunferência.

Assim, dados um plano α{displaystyle alpha }, um ponto O{displaystyle O} e uma distância r{displaystyle r}, temos:

λ(O,r)={P∈α/dP,O=r}{displaystyle lambda left(O,rright)=left{Pin alpha /quad {d_{P,O}=r}right}}^[2],

onde λ(O,r){displaystyle lambda left(O,rright)} representa a circunferência de centro O{displaystyle O} e raio r{displaystyle r}.

Uma circunferência λ{displaystyle lambda } de raio r{displaystyle r} e centro O{displaystyle O}.

Posições relativas entre ponto e circunferência |

Exemplo de posições relativas entre pontos e circunferência: A{displaystyle A} é ponto interno a circunferência; B{displaystyle B} está sob a circunferência e C{displaystyle C} é ponto externo à circunferência.

Dado um ponto X{displaystyle X} e uma circunferência λ(O,r){displaystyle lambda left(O,rright)}, temos

• 
  Xé interno a λ⟺dX,O<r{displaystyle Xquad {text{é interno a }}lambda qquad Longleftrightarrow quad {d_{X,O}<r}}, ou seja, um ponto qualquer é interno a uma circunferência se, e somente se, a distância desse ponto até o centro da circunferência é menor do que o raio da circunferência.


• 
  Xpertence a λ⟺dX,O=r{displaystyle Xquad {text{pertence a }}lambda qquad Longleftrightarrow quad {d_{X,O}=r}}, ou seja, um ponto qualquer pertence (ou está sobre) a uma circunferência se, e somente se, a distância desse ponto até o centro da circunferência é igual ao raio da circunferência.


• 
  Xé externo a λ⟺dX,O>r{displaystyle Xquad {text{é externo a }}lambda qquad Longleftrightarrow quad {d_{X,O}>r}}, ou seja, um ponto qualquer é externo a uma circunferência se, e somente se, a distância desse ponto até o centro da circunferência é maior do que o raio da circunferência.

Assim, com base nessas definições, podemos definir interior e exterior de uma circunferência.

O interior de uma circunferência é o conjunto dos pontos internos a ela e o exterior de uma circunferência é o conjunto de pontos externos a ela.

Quando unimos o interior de uma circunferência à própria circunferência temos um círculo ou um disco. Logo, um círculo é um conjunto dos pontos de um plano cuja distância a um ponto dado nesse plano é menor ou igual a uma distância (não nula) dada.

Corda, diâmetro e raio |

Ver artigo principal: Corda (geometria)

Corda, diâmetro e raio são segmentos que estão associados a uma circunferência.

Corda |

Corda de uma circunferência é um segmento cujas extremidades pertencem à circunferência.

Diâmetro |

Diâmetro de uma circunferência é uma corda que passa pelo centro da circunferência, a maior corda da mesma, também sendo o dobro do raio.

Raio |

Raio de uma circunferência é um segmento com uma extremidade no centro e outra num ponto da circunferência.

Exemplos de corda, diâmetro e raio de uma circunferência: Raio AO¯{displaystyle {overline {AO}}}, Diâmetro BC¯{displaystyle {overline {BC}}} e Corda ED¯{displaystyle {overline {ED}}}.

Arco de circunferência |

Dois arcos congruentes.

Adição de dois arcos

Desigualdade de Arcos: AB^>CD^{displaystyle {widehat {AB}}>{widehat {CD}}}

Ver artigo principal: Arco (matemática)

Arco de circunferência é uma parte do comprimento da circunferência delimitado por dois pontos quaisquer (que são os extremos do arco).^[3]

De maneira mais formal, consideremos uma circunferência λ{displaystyle lambda } de centro O{displaystyle O} e, sejam A{displaystyle A} e B{displaystyle B} dois pontos de λ{displaystyle lambda } que não sejam extremidades de um diâmetro, temos:

1. Arco menor AB^{displaystyle {widehat {AB}}} é a reunião dos conjuntos dos pontos {A}{displaystyle {A}}, {B}{displaystyle {B}} e de todos os pontos de λ{displaystyle lambda } que estão no interior do ângulo AO^B{displaystyle A{hat {O}}B}.


2. Arco maior AB^{displaystyle {widehat {AB}}} é a reunião dos conjuntos dos pontos {A}{displaystyle {A}}, {B}{displaystyle {B}} e de todos os pontos de λ{displaystyle lambda } que estão no exterior do ângulo AO^B{displaystyle A{hat {O}}B}.^[2]
   

Arcos congruentes |

Dois arcos AB^{displaystyle {widehat {AB}}} e CD^{displaystyle {widehat {CD}}} de uma circunferência de centro O{displaystyle O} são congruentes se, e somente se, os ângulos AO^B{displaystyle A{hat {O}}B} e CO^D{displaystyle C{hat {O}}D} são congruentes.

Ou seja:

AB^≡CD^⟺AO^B≡CO^D{displaystyle {widehat {AB}}equiv {widehat {CD}}qquad Longleftrightarrow qquad {A{hat {O}}Bequiv {C{hat {O}}D}}}

Adição de arcos |

Numa circunferência de centro O{displaystyle O}, o arco AB^{displaystyle {widehat {AB}}} é a soma dos arcos AC^{displaystyle {widehat {AC}}} e CB^{displaystyle {widehat {CB}}} se, e somente se, o ângulo AO^B{displaystyle A{hat {O}}B} é soma dos ângulos AO^C{displaystyle A{hat {O}}C} e CO^B{displaystyle C{hat {O}}B}.

Ou seja:

AB^=AC^+CB^⟺AO^B=AO^C+CO^B{displaystyle {widehat {AB}}={widehat {AC}}+{widehat {CB}}qquad Longleftrightarrow qquad {A{hat {O}}B=A{hat {O}}C+C{hat {O}}B}}

Desigualdade de arcos |

Numa circunferência de centro O{displaystyle O}, o arco AB^{displaystyle {widehat {AB}}} é maior que o arco CD^{displaystyle {widehat {CD}}} se, e somente se, o ângulo AO^B{displaystyle A{hat {O}}B} é maior que o ângulo CO^D{displaystyle C{hat {O}}D}.

Ou seja:

AB^>CD^⟺AO^B>CO^D{displaystyle {widehat {AB}}>{widehat {CD}}qquad Longleftrightarrow qquad {A{hat {O}}B>C{hat {O}}D}}^[2]

Setor circular e segmento circular |

Para essas definição vamos considerar um círculo c{displaystyle c} de centro O{displaystyle O} e sejam A{displaystyle A} e B{displaystyle B} dois pontos na circunferência de c{displaystyle c} que não sejam extremidades de um diâmetro.

Setor circular |

Ver artigo principal: Setor circular

• 
  Setor circular menor AOB{displaystyle AOB} é a reunião dos conjuntos dos pontos dos raios OA¯{displaystyle {overline {OA}}} e OB¯{displaystyle {overline {OB}}} e de todos os pontos do círculo c{displaystyle c} que estão no interior do ângulo AO^B{displaystyle A{hat {O}}B}.


• 
  Setor circular maior AOB{displaystyle AOB} é a reunião dos conjuntos dos pontos dos raios OA¯{displaystyle {overline {OA}}} e OB¯{displaystyle {overline {OB}}} e de todos os pontos do círculo c{displaystyle c} que estão no exterior do ângulo AO^B{displaystyle A{hat {O}}B}.

Segmento circular |

Ver artigo principal: Segmento circular

Segmento circular menor AB{displaystyle AB} é a intersecção do círculo c{displaystyle c} com o semiplano de origem na reta AB↔{displaystyle {overleftrightarrow {AB}}} e que não contém o centro de c{displaystyle c}.

Segmento circular maior AB{displaystyle AB} é a intersecção do círculo c{displaystyle c} com o semiplano de origem na reta AB↔{displaystyle {overleftrightarrow {AB}}} e que contém o centro de c{displaystyle c}.

Posições relativas entre reta e circunferência |

Dados uma reta r{displaystyle r} e uma circunferência λ{displaystyle lambda } em um plano qualquer, podemos ter apenas uma das duas condições abaixo:

• 
  r{displaystyle r} é secante a λ{displaystyle lambda };


• 
  r{displaystyle r} é tangente a λ{displaystyle lambda }.


• 
  r{displaystyle r} é exterior a λ{displaystyle lambda }
  

Secante |

Reta secante a uma circunferência

Uma reta é secante a uma circunferência quando elas se interceptam em dois pontos distintos.

Assim dizemos que a reta e a circunferência são secantes.

r∩λ={A,B}{displaystyle rcap lambda ={A,B}}

Toda reta secante a uma circunferência define uma corda na mesma circunferência.

Propriedades da secante |

Como toda reta secante define uma corda em uma circunferência, nessas propriedades, trataremos que as cordas e as retas secantes possuem as mesmas propriedades.

• Toda corda é perpendicular ao raio da circunferência em seu ponto médio.


• Todo raio que passa pelo ponto médio de uma corda é perpendicular a mesma corda.

Assim, essa propriedade pode ser interpretada como sendo a "ida" e a volta do mesmo "teorema", que afirma, sem perda de generalidade que:

"Uma reta é secante a uma circunferência se, e somente se, é perpendicular ao raio da circunferência no ponto médio da corda definida pela intersecção da reta com a circunferência."^[2]

Demonstração |

Imagem suporte para primeira parte da demonstração

Primeira parte |

Primeiramente vamos demonstrar que toda corda é perpendicular ao raio da circunferência em seu ponto médio.

Ou seja, vamos demonstrar o seguinte teorema:

A,B∈λ(O,r),M é ponto médio de AB¯⟹OM¯⊥AB¯{displaystyle A,Bin lambda (O,r),quad {M}{text{ é ponto médio de }}{overline {AB}}qquad Longrightarrow qquad {{overline {OM}}perp {overline {AB}}}}

Para fazer essa demonstração vamos observar os triângulos △AMO{displaystyle triangle {AMO}} e △BMO{displaystyle triangle {BMO}}.

Pode-se observar que esses triângulos são congruentes, da seguinte forma:

OA¯≡OB¯,OM¯≡OM¯eAM¯≡MB¯(LLL)⟹△AMO≡△BMO{displaystyle {overline {OA}}equiv {overline {OB}},quad {overline {OM}}equiv {overline {OM}}quad {text{e}}quad {overline {AM}}equiv {overline {MB}}quad left(LLLright)qquad Longrightarrow qquad triangle {AMO}equiv triangle {BMO}}.

Assim, temos que AM^O≡BM^O{displaystyle A{hat {M}}Oequiv {B{hat {M}}O}}.

Temos também que esses dois ângulos são suplementares, visto que um é o ângulo externo adjacente ao outro.

Assim temos:

med(AM^O)+med(BM^O)=180∘⟹2.med(AM^O)=180∘⟹med(AM^O)=90∘{displaystyle medleft(A{hat {M}}Oright)+medleft(B{hat {M}}Oright)=180^{circ }qquad Longrightarrow qquad {2.medleft(A{hat {M}}Oright)}=180^{circ }qquad Longrightarrow qquad {medleft(A{hat {M}}Oright)}=90^{circ }}

Imagem suporte para segunda parte da demonstração

Logo, OM¯≡AB¯{displaystyle {overline {OM}}equiv {overline {AB}}}.

Tento isso demonstrado, podemos afirmar, sem perda de generalidade que toda reta secante é perpendicular ao raio no ponto médio da corda que define na circunferência.

Segunda parte |

Agora vamos demonstrar que todo raio que passa pelo ponto médio de uma corda é perpendicular a mesma corda.

Ou seja, vamos demonstrar o seguinte teorema:

A,B∈λ(O,r),OM¯⊥AB¯,M∈AB¯⟹AM¯≡MB¯{displaystyle A,Bin lambda (O,r),quad {overline {OM}}perp {overline {AB}},quad {M}in {overline {AB}}qquad Longrightarrow qquad {{overline {AM}}equiv {overline {MB}}}}

Para fazer essa demonstração vamos observar os triângulos △AMO{displaystyle triangle {AMO}} e △BMO{displaystyle triangle {BMO}}.

Visto que esses dois triângulos são triângulos retângulos, podemos facilmente verificar sua congruência, da seguinte forma:

OA¯≡OB¯eOM¯≡OM¯(CH)⟹△AMO≡△BMO{displaystyle {overline {OA}}equiv {overline {OB}}quad {text{e}}quad {overline {OM}}equiv {overline {OM}}quad left(CHright)qquad Longrightarrow qquad triangle {AMO}equiv triangle {BMO}}

Dessa congruência temos que AM¯≡MB¯{displaystyle {overline {AM}}equiv {overline {MB}}}, que significa que M{displaystyle M} é ponto médio de AB¯{displaystyle {overline {AB}}}.

Com essas duas demonstrações podemos afirmar, sem perda de generalidade que:

"Uma reta é secante a uma circunferência se, e somente se, é perpendicular ao raio da circunferência no ponto médio da corda que define."

Tangente |

Uma reta e uma circunferência são tangentes quando se interceptam em apenas um ponto. A esse ponto comum damos o nome de ponto de tangência.

r∩λ={T}{displaystyle rcap lambda ={T}}

Reta tangente a uma circunferência

Propriedades da tangente |

Quanto a retas tangentes à circunferências temos duas propriedades, que na verdade são a "ida" e a "volta" do mesmo teorema:

• Toda reta perpendicular a um raio na sua extremidade da circunferência é tangente à circunferência.


• Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.

Então, essas duas propriedades podem ser enunciadas sob forma de um único teorema:

"Uma reta é tangente a uma circunferência se, e somente se, é perpendicular ao raio no ponto de tangência."^[2]

Demonstração |

Primeira parte |

Reta perpendicular a uma circunferência

Primeiramente vamos demonstrar a primeira parte do teorema, que pode se enunciada da seguinte forma, onde λ{displaystyle lambda } é uma circunferência de centro O{displaystyle O} e s{displaystyle s} uma reta.

A∈λ,s⊥OA¯es∩OA¯={A}⟹s∩λ={A}{displaystyle Ain lambda ,quad {s}perp {overline {OA}}quad {text{e}}quad {s}cap {overline {OA}}={A}qquad Longrightarrow qquad {s}cap lambda ={A}}

Para demonstrar essa proposição utilizaremos demonstração por absurdo.

Assim, partiremos admitindo que há pelo menos dois pontos na intersecção entre a reta e a circunferência e buscaremos alguma contradição a partir disso. Ou seja: s∩λ={A,B}{displaystyle scap lambda ={A,B}}.

Imagem suporte da primeira parte da demonstração

A partir disso, temos:

A,B∈λ⟹OA¯≡OB¯⟹△OABé isósceles⟹OA^B≡OB^A(I){displaystyle A,Bin lambda qquad Longrightarrow qquad {overline {OA}}equiv {overline {OB}}qquad Longrightarrow qquad triangle {OAB}quad {text{é isósceles}}qquad Longrightarrow qquad {O{hat {A}}Bequiv {O{hat {B}}A}}qquad left(Iright)}

Pela hipótese temos:

s⊥OA¯⟹med(OA^B)=90∘(II){displaystyle sperp {overline {OA}}qquad Longrightarrow qquad {medleft(O{hat {A}}Bright)}=90^{circ }left(IIright)}

De (I){displaystyle left(Iright)} e (II){displaystyle left(IIright)} encontramos nossa contradição, pois temos um triângulo que possui dois ângulos retos na base.

Logo s∩λ={A}{displaystyle scap lambda ={A}}, o que significa que a reta e a circunferência são tangentes.

Segunda parte |

Imagem suporte para segunda parte da demonstração

Agora queremos demonstrar que se uma reta é tangente a uma circunferência, então ela é perpendicular ao raio no ponto de tangência, ou seja, queremos demonstrar:

s∩λ={A}⟹s⊥OA¯{displaystyle scap lambda ={A}qquad Longrightarrow qquad {sperp {overline {OA}}}}

Para demonstrar essa afirmação iniciaremos supondo que s{displaystyle s} não seja perpendicular a OA¯{displaystyle {overline {OA}}} e assim entraremos em contradição com a nossa hipótese.

Assim, se s{displaystyle s} não for perpendicular a OA¯{displaystyle {overline {OA}}} podemos tomar um ponto M∈s{displaystyle Min {s}} de modo que OM¯⊥s{displaystyle {overline {OM}}perp {s}} de modo que M{displaystyle M} e A{displaystyle A} sejam distintos.

Agora tomaremos na semirreta oposta a MA→{displaystyle {overrightarrow {MA}}} um ponto B{displaystyle B} tal que MB¯≡MA¯{displaystyle {overline {MB}}equiv {overline {MA}}}.

Imagem suporte para segunda parte da demonstração

A partir disso podemos verificar a congruência de triângulos que segue:

OM¯≡OM¯,OM¯⊥MA¯eMB¯≡MA¯(LAL)⟹△OMB≡△OMA{displaystyle {overline {OM}}equiv {overline {OM}},quad {overline {OM}}perp {overline {MA}}quad {text{e}}quad {overline {MB}}equiv {overline {MA}}quad left(LALright)qquad Longrightarrow qquad triangle {OMB}equiv triangle {OMA}}.

Visto que os dois triângulos são congruentes, temos que seus respectivos lados também são.

Assim, temos que OB¯≡OA¯{displaystyle {overline {OB}}equiv {overline {OA}}}.

Como OA¯{displaystyle {overline {OA}}} é raio da circunferência, temos que OB¯{displaystyle {overline {OB}}} também é, o que implica B∈λ{displaystyle Bin lambda }.

Então temos que s∩λ={A,B}{displaystyle scap lambda ={A,{B}}}, o que contradiz nossa hipótese de que a reta seja tangente à circunferência.

Logo, se uma reta é tangente a uma circunferência, então ela é também perpendicular ao raio da circunferência no ponto de tangência.

Tendo isso demonstrado podemos afirmar:

"Uma reta é tangente a uma circunferência se, e somente se, é perpendicular ao raio da circunferência no ponto de tangência."^[2]

Exterior |

Uma reta é exterior a uma circunferência quando as duas não se interceptam, ou seja, sua intersecção é vazia.

r∩λ=∅{displaystyle rcap lambda =varnothing }

Uma reta exterior a uma circunferência

Posições relativas entre duas circunferências |

Quanto a posição relativa entre duas circunferências é comum classificar quanto a quantidade de intersecções que duas circunferências podem ter.

Assim temos que duas circunferências podem ser coincidentes, secantes, tangentes ou não possuírem intersecção.

Além disso, duas circunferências podem ser também concêntricas, quando seus centros são coincidentes.

Se, além de serem concêntricas elas tiverem o mesmo raio dizemos que elas são coincidentes (ou que são a mesma circunferência).

Circunferências em posições relativas: 1. Distintas, 2. Tangência externa, 3. Secantes, 4. Tangência interna e 5. Concêntricas.

Circunferências tangentes |

Duas circunferências são tangentes quando possuem apenas um ponto em comum, ou seja:

λ1e λ2 são tangentes ⟺λ1∩λ2={T}{displaystyle lambda _{1}{text{e }}lambda _{2}{text{ são tangentes }}qquad Longleftrightarrow qquad lambda _{1}cap lambda _{2}={T}}

Tangentes internas |

Uma circunferência é tangente interna a outra se têm apenas um ponto em comum e todos os demais pontos de uma são internos a outra.

Isso ocorre quando a distância entre os centros é igual à diferença dos raios das circunferências:

λ1(O1,r1) é tangente interior a λ2(O2,r2)⟺dO1,O2=|r1−r2|{displaystyle lambda _{1}left(O_{1},r_{1}right){text{ é tangente interior a }}lambda _{2}left(O_{2},r_{2}right)qquad Longleftrightarrow qquad {d_{O_{1},O_{2}}=|r_{1}-r_{2}|}}

Tangentes externas |

Uma circunferência é tangentes externas a outra se têm apenas um ponto em comum e todos os demais pontos de uma são externos a outra.^[4]

Isso ocorre quando a distância entre o centros é igual à soma dos raios das circunferências:

λ1(O1,r1) é tangente exterior a λ2(O2,r2)⟺dO1,O2=r1+r2{displaystyle lambda _{1}left(O_{1},r_{1}right){text{ é tangente exterior a }}lambda _{2}left(O_{2},r_{2}right)qquad Longleftrightarrow qquad {d_{O_{1},O_{2}}=r_{1}+r_{2}}}

Circunferências secantes |

Duas circunferências são secantes quando possuem dois, e apenas dois, pontos em comum, ou seja:

λ1e λ2 são secantes ⟺λ1∩λ2={A,B}{displaystyle lambda _{1}{text{e }}lambda _{2}{text{ são secantes }}qquad Longleftrightarrow qquad lambda _{1}cap lambda _{2}={A,B}}

Diferentemente de quando falamos de circunferências tangentes, quando tratamos de circunferências secantes não faz sentido falar de secantes internas ou externas.

Isso ocorre quando a distância entre os centros é maior que o módulo da diferença dos raios e menor que a soma dos raios:

λ1(O1,r1) é secante a λ2(O2,r2)⟺|r1−r2|<dO1,O2<r1+r2{displaystyle lambda _{1}left(O_{1},r_{1}right){text{ é secante a }}lambda _{2}left(O_{2},r_{2}right)qquad Longleftrightarrow qquad {|r_{1}-r_{2}|}<{d_{O_{1},O_{2}}<r_{1}+r_{2}}}

Circunferências sem pontos em comum |

Circunferências sem pontos em comum são, simplesmente, circunferências cuja intersecção entre ambas é vazia.

Assim, quando a intersecção entre duas circunferências é vazia temos que: ou elas são externas ou uma é interna a outra.

Circunferências externas |

Duas circunferências são externas se os pontos de uma são externos a outra.

Isso ocorre quando a distância entre os centros é maior que a diferença dos raios da circunferência:

λ1(O1,r1)eλ2(O2,r2)são externas⟺dO1,O2>r1+r2{displaystyle lambda _{1}left(O_{1},r_{1}right)quad {text{e}}quad lambda _{2}left(O_{2},r_{2}right)quad {text{são externas}}qquad Longleftrightarrow qquad {d_{O_{1},O_{2}}>r_{1}+r_{2}}}

Circunferências internas |

Uma circunferência é interna a outra se todos os seus pontos são pontos internos da outra.

Isso ocorre quando a distância entre o centros é menor que a soma dos raios da circunferência:

λ1(O1,r1) interior a λ2(O2,r2)⟺dO1,O2<r2−r1{displaystyle lambda _{1}left(O_{1},r_{1}right){text{ interior a }}lambda _{2}left(O_{2},r_{2}right)qquad Longleftrightarrow qquad {d_{O_{1},O_{2}}<r_{2}-r_{1}}}

No caso das circunferências concêntricas, que foram citadas anteriormente, percebe-se que elas são um caso particular de circunferências internas, onde O1=O2{displaystyle O_{1}=O_{2}}.

Segmentos tangentes conduzidos de um mesmo ponto |

Se de um ponto P{displaystyle P} conduzirmos os segmentos PA¯{displaystyle {overline {PA}}} e PB¯{displaystyle {overline {PB}}}, ambos pertencentes a retas distintas e tangentes a uma circunferência, com A{displaystyle A} e B{displaystyle B} na circunferência, então PA¯≡PB¯{displaystyle {overline {PA}}equiv {overline {PB}}}.^[2]

Demonstração |

Queremos demonstrar que:

PA¯ePB¯tangentes a λ;A,B∈λ⟹PA¯≡PB¯{displaystyle {overline {PA}}quad {text{e}}quad {overline {PB}}quad {text{tangentes a }}lambda ;quad {A,B}in lambda qquad Longrightarrow qquad {overline {PA}}equiv {overline {PB}}}

Seja O{displaystyle O} o centro de λ{displaystyle lambda }, podemos traçar o segmento OP¯{displaystyle {overline {OP}}} e observar que, assim, surgem dois triângulos: △PAO{displaystyle triangle {PAO}} e △PBO{displaystyle triangle {PBO}}.

Pelo fato de A{displaystyle A} e B{displaystyle B} pertencerem a circunferência temos OA¯≡OB¯{displaystyle {overline {OA}}equiv {overline {OB}}} e, pelo fato de PA↔{displaystyle {overleftrightarrow {PA}}} e PB↔{displaystyle {overleftrightarrow {PB}}} serem tangente a λ{displaystyle lambda }, o que nos garante que OA^P{displaystyle O{hat {A}}P} e OB^P{displaystyle O{hat {B}}P} são ângulos retos.

Assim temos que esses dois triângulos são triângulos retângulos que possuem um cateto e a hipotenusa congruentes, o que implica os triângulos serem congruentes:

OA¯≡OB¯eOP¯≡OP¯(CH)⟹△PAO≡△PBO{displaystyle {overline {OA}}equiv {overline {OB}}quad {text{e}}quad {overline {OP}}equiv {overline {OP}}quad left(CHright)qquad Longrightarrow qquad triangle {PAO}equiv triangle {PBO}}.

Como os dois triângulos são congruentes, temos que:

PA¯≡PB¯{displaystyle {overline {PA}}equiv {overline {PB}}}.

Equações |

Uma circunferência pode ser representada por equações algébricas.

Coordenadas retangulares |

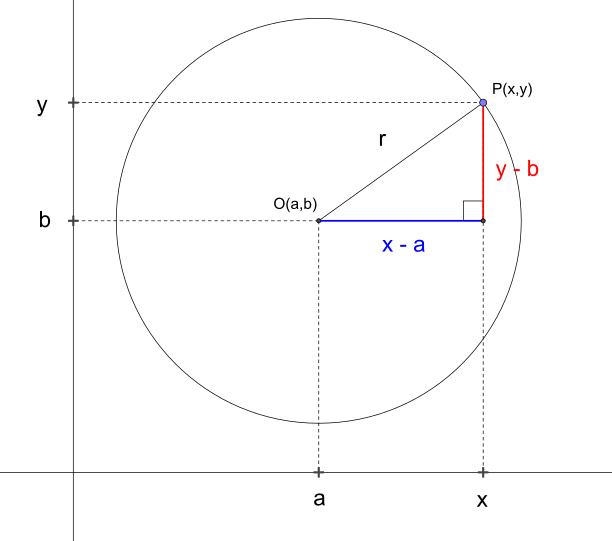
Num sistema de coordenadas cartesianas retangulares, uma circunferência pode ser descrita pela equação^[5]

(x−a)2+(y−b)2=r2,{displaystyle (x-a)^{2}+(y-b)^{2}=r^{2},,}

na qual a{displaystyle a} e b{displaystyle b} são as coordenadas do centro da circunferência e r{displaystyle r} é o raio. Caso a circunferência tenha o centro sobre a origem do plano cartesiano, a equação é

x2+y2=r2.{displaystyle x^{2}+y^{2}=r^{2},.}

Demonstração |

Vamos demonstrar que uma circunferência λ{displaystyle lambda } de raio r{displaystyle r} e centrada no ponto O(a,b){displaystyle Oleft(a,bright)} é

(x−a)2+(y−b)2=r2.{displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}quad .}

Por definição temos que uma circunferência é o conjunto de todos os pontos de um plano que são equidistantes a um dado ponto nesse plano.

Assim, podemos definir λ{displaystyle lambda } da seguinte forma:

λ={P(x,y)∈R2|dO,P=r}{displaystyle lambda ={{Pleft(x,yright)in mathbb {R} ^{2}}|quad {d_{O,P}}=r}}

Pela fórmula da distância entre dois pontos, da geometria analítica (ou simplesmente analisando o triângulo retângulo, como mostra a figura ao lado), temos:

dP,O=r⟺(x−a)2+(y−b)2=r2{displaystyle {d_{P,O}=r}qquad Longleftrightarrow qquad {left(x-aright)^{2}+left(y-bright)^{2}=r^{2}}}

Equações paramétricas |

Também é possível descrever uma circunferência através de equações paramétricas, em função de um parâmetro t{displaystyle t} e usando funções trigonométricas:

x=a+rcos(t){displaystyle x=a+rcos(t)}

y=b+rsen(t).{displaystyle y=b+rsen(t),.}

Ou simplesmente com uma circunferência λ{displaystyle lambda } de raio r{displaystyle r} e centrada em O(a,b){displaystyle Oleft(a,bright)}sendo o conjunto de vetores:

λ={(a+r.cos⁡(t),b+r.sen⁡(t))∈R2,0≤t≤2π}{displaystyle lambda ={left(a+r.cos(t),b+r.operatorname {sen} (t)right)in mathbb {R} ^{2},quad 0leq {t}leq 2pi }}

Neste caso, t{displaystyle t} é a variável paramétrica, variando entre 0 e 2π{displaystyle pi } radianos.

Na geometria analítica, pode ser representada através de uma equação da forma Ax2+By2+Cxy+Dx+Ey+F=0{displaystyle Ax^{2}+By^{2}+Cxy+Dx+Ey+F=0}, com coeficientes reais. Sendo que A{displaystyle A} deve ser igual a B{displaystyle B} e diferente de zero e C{displaystyle C} deve ser igual a zero. O raio da circunferência é obtido através da relação:

R2=D2+E2−4A.F4A2{displaystyle R^{2}={frac {D^{2}+E^{2}-4A.F}{4A^{2}}}}.

Perímetro |

A extensão da circunferência, ou seja, seu perímetro, c{displaystyle c}, pode ser calculada através da equação^[1]

c=πd=2r π,{displaystyle c=pi d=2r pi ,}

em que d{displaystyle d} é o diâmetro da circunferência, ou seja, o dobro de seu raio:

d=2r.{displaystyle d=2r,.}

Também temos π{displaystyle pi } (pron. pi) que é a constante, cujo valor é

π=3,14...{displaystyle pi =3,14...}

Uma circunferência com raio 1 unidade tem perímetro de comprimento 2π.

Círculo |

O círculo é a área interna (a{displaystyle a}) delimitada pela circunferência^[1], que pode ser calculada usando a equação

a=πr2 =πd2/4.{displaystyle a=pi r^{2} =pi d^{2}/4.}

Seção cônica |

A circunferência é a curva plana fechada que se obtém quando da interseção de um cone circular reto com um plano paralelo à sua base.^[6]

Seções cônicas: A = Parábola, B = Circunferência (parte de baixo do duplo cone) e Elipse (parte de cima), C = Hipérboles

Referências

Ver também |

• Lugares geométricos


• Círculo


• Diâmetro


• Retificação da circunferência


• Trigonometria

Bibliografia |

• 
  Braga, Theodoro - Desenho linear geométrico. Ed. Cone, São Paulo: 1997.


• 
  Carvalho, Benjamim - Desenho Geométrico. Ed. Ao Livro Técnico, São Paulo: 1982.


• 
  Giongo, Affonso Rocha - Curso de Desenho Geométrico. Ed. Nobel, São Paulo: 1954.


• 
  Mandarino, Denis - Desenho Geométrico, construções com régua e compasso. Ed. Plêiade, São Paulo: 2007.


• Marmo, Carlos - Desenho Geométrico. Ed. Scipione, São Paulo: 1995.


• Putnoki, José Carlos - Elementos de geometria e desenho geométrico. Vol. 1 e 2. Ed. Scipione, São Paulo: 1990.

Ligações externas |

• 
  Alfred North Whitehead: An Introduction to Mathematics. BiblioBazaar LLC 2009 (reprint), ISBN 9781103197842, pp. 121 [1]
  


• George Wentworth: Junior High School Mathematics: Book III. BiblioBazaar LLC 2009 (reprint), ISBN 9781103152360, pp. 265 [2]
  


• Robert Clarke James, Glenn James: Mathematics Dictionary. Springer 1992, ISBN 9780412990410, p. 255 [3]